Chapter 07.06: Integrating Functions Given as Discrete Data Points
Learning Objectives
After successful completion of this lesson, you should be able to:
1) derive the formula for the trapezoidal rule with unequal segments
2) estimate integrals of functions given at discrete data points.
Introduction
Most functions to be integrated may not be given mathematically as continuous functions. They may be only given at discrete data points. Such functions have to be integrated numerically. One technique to do so is an extension of the single-segment trapezoidal rule and is called the “Trapezoidal rule with unequal segments.”
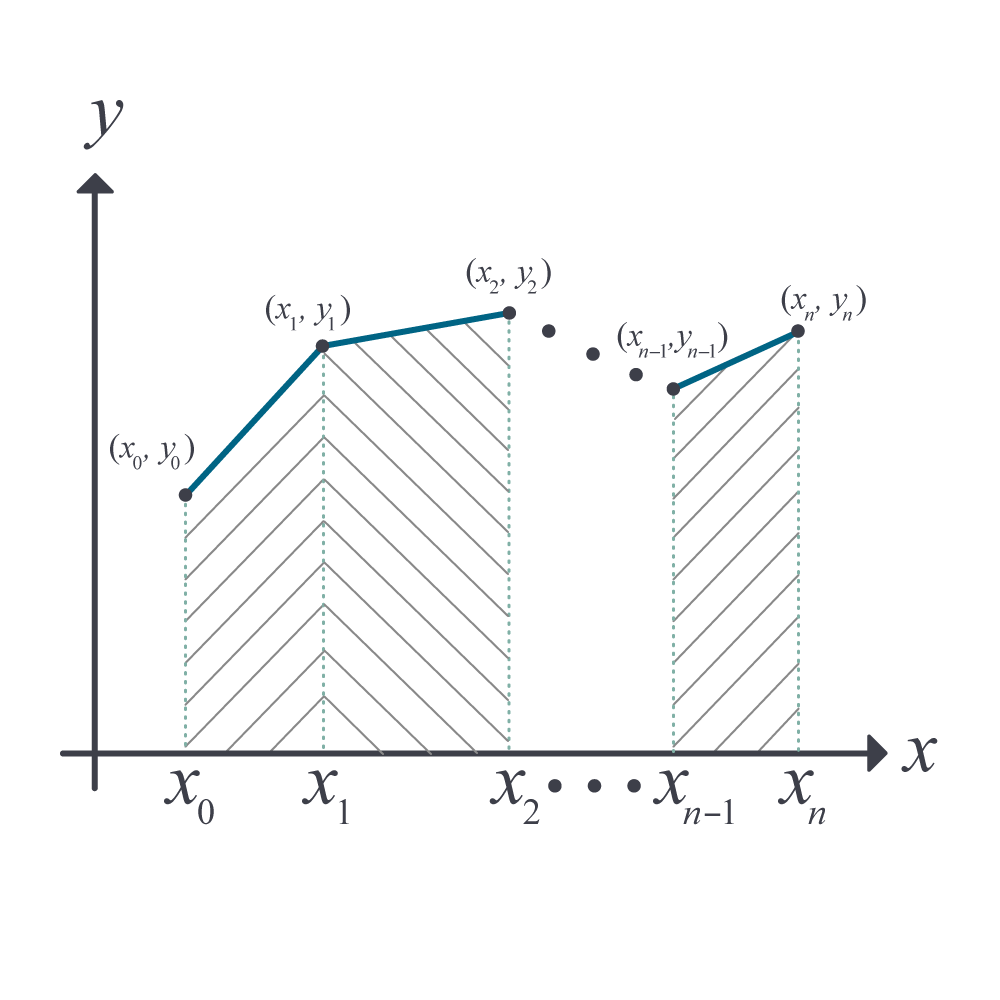
Figure 1. Illustration of trapezoidal rule with unequal segments.
For a general case of a function given at \(n\) data points \(\left( x_{1},f\left( x_{1} \right) \right),\ \left( x_{2},f\left( x_{2} \right) \right),\ \left( x_{3},f\left( x_{3} \right) \right), \ldots,\ \left( x_{n},\ f\left( x_{n} \right) \right)\), where, \(x_{1},.x_{2},\ldots,x_{n}\) are in ascending order, the integral\(\displaystyle \int_{x_{1}}^{x_{n}}{f\left( x \right)}{dx }\) can be broken into \(n - 1\) separate integrals
\[\int_{x_{1}}^{x_{n}}{f\left( x \right)}dx = \int_{x_{1}}^{x_{2}}{f\left( x \right)}dx + \int_{x_{2}}^{x_{3}}{f\left( x \right)}dx + ...... + \int_{x_{n - 1}}^{x_{n}}{f\left( x \right)}{dx}\]
Using a single-segment trapezoidal rule for each integral (Figure 1) gives
\[\begin{split} \int_{x_{1}}^{x_{n}}{f\left( x \right)}{dx} &\approx \left( x_{2} - x_{1} \right)\frac{f\left( x_{1} \right) + f\left( x_{2} \right)}{2} + \left( x_{3} - x_{2} \right)\frac{f\left( x_{2} \right) + f\left( x_{3} \right)}{2} + ......\\ & \ \ \ \ \ \ ....... + \left( x_{n} - x_{n - 1} \right)\frac{f\left( x_{n - 1} \right) + f\left( x_{n} \right)}{2}\\ &= \sum_{i = 1}^{n - 1}{\left( x_{i + 1} - x_{i} \right)\frac{f\left( x_{i} \right) + f\left( x_{i + 1} \right)}{2}}\;\;\;\;\;\;\;\;\;\;\;\; (1) \end{split}\]
Equation (1) estimates an integral of a function given at discrete data points using trapezoidal rule with unequal segments.
Example 1
The upward velocity of a rocket is given as a function of time in Table 1.
Table 1 Velocity as a function of time.
| \(t(\text{s})\) | \(v(t)(\text{m/s})\) |
|---|---|
| \(0\) | \(0\) |
| \(10\) | \(227.04\) |
| \(15\) | \(362.78\) |
| \(20\) | \(517.35\) |
| \(22.5\) | \(602.97\) |
| \(30\) | \(901.67\) |
Using the trapezoidal rule with unequal segments, determine the distance, \(s,\) covered by the rocket from \(t = 10\) to \(t = 20\) seconds.
Solution
To find the distance covered from \(t = 10\) to \(t = 20\) seconds
\[\int_{10}^{20}v(t)= \int_{10}^{15}{v(t)dt} + \int_{15}^{20}{v(t)dt}\]
and applying the trapezoidal rule over each of the above integrals gives
\[\begin{split} \int_{10}^{20}{v(t){dt}} &\approx \frac{15 - 10}{2}\lbrack v(10) + v(15) \rbrack + \frac{20 - 15}{2}\lbrack v(15) + v(20)\rbrack\\ &= 2.5(227.04+362.78)+2.5(362.78+517.35)\\ &= 3674.875\ \text{m} \end{split}\]
How would you use the trapezoidal rule with unequal segments if the integral to be found has the limits of integration where one or both the limits are not a given data point? An example is given below to solve such a problem.
Example 2
The upward velocity of a rocket is given as a function of time in Table 1.
Table 1 Velocity as a function of time.
| \(t(\text{s})\) | \(v(t)(\text{m/s})\) |
|---|---|
| \(0\) | \(0\) |
| \(10\) | \(227.04\) |
| \(15\) | \(362.78\) |
| \(20\) | \(517.35\) |
| \(22.5\) | \(602.97\) |
| \(30\) | \(901.67\) |
Using the trapezoidal rule with unequal segments, determine the distance, \(s,\) covered by the rocket from \(t = 11\) to \(t = 16\) seconds.
Solution Here, we are asked to estimate the distance covered from \(t = 11\) to \(t = 16\).
\[\int_{11}^{16}{v(t)dt} = \int_{11}^{15}{v(t)dt} + \int_{15}^{16}{v(t)dt}\]
and applying the trapezoidal rule over each of the above integrals gives
\[\begin{split} \int_{11}^{16}{v\left( t \right){dt}} &\approx \frac{15 - 11}{2}\left\lbrack v\left( 11 \right) + v\left( 15 \right) \right\rbrack + \frac{16 - 15}{2}\lbrack v(15) + v(16)\rbrack\\ &= \frac{15 - 11}{2}\left( v\left( 11 \right) + 362.78 \right) + \frac{16 - 15}{2}\left( 362.78 + v\left( 16 \right) \right) \end{split}\]
How do we find \(v(11)\) and \(v(16)\)? We use linear interpolation with a simple formula, which is, given \((t_{0},v_{0})\) and \((t_{1},v_{1})\), the straight line that passes through the two points is given by
\[v = v_{0} + \frac{v_{1} - v_{0}}{t_{1} - t_{0}}(t - t_{0}),\ t_{0} \leq t \leq t_{1}\]
To find \(v(11)\), we choose the closest two points that bracket \(t=11\), and those two points are \(t=10\) and \(t=15\).
\[\begin{split} v(t) &=v(10)+\frac{v(15)-v(10)}{15-10}(t-10),\ 10\leq\ t\leq 15 \\ &=227.04+\frac{362.78-227.04}{15-10}\left(t-10\right),\ 10\le t\le15\\ &= 227.04 + 27.148\left( t - 10 \right),\ 10 \leq t \leq 15 \end{split}\]
Then
\[\begin{split} v(11) &= 227.04 + 27.148\left( 11 - 10 \right)\\ &= 254.19\ \text{m/s} \end{split}\]
To find \(v(16)\), we choose the two closest points that bracket \(t=16\), and those two points are \(t=15\) and \(t=20\).
\[\begin{split} v\left( t \right) &= v\left( 15 \right) + \frac{v\left( 20 \right) - v\left( 15 \right)}{20 - 15}\left( t - 15 \right),15 \leq t \leq 20\\ &= 362.78 + \frac{517.35 - 362.784}{20 - 15}\left( t - 15 \right),15 \leq t \leq 20\\ &= 362.78 + 30.913\left( t - 15 \right),15 \leq t \leq 20 \end{split}\]
Then
\[\begin{split} v(16) &= 362.78 + 30.913\left( 16 - 15 \right)\\ &= 393.69\ \text{m/s} \end{split}\]
So
\[\begin{split} \int_{11}^{16}v\left( t \right){dt} &\approx \frac{15 - 11}{2}\left( v\left( 11 \right) + 362.78 \right) + \frac{16 - 15}{2}(362.78 + v(16))\\ &= \frac{15 - 11}{2}(254.19 + 362.78) + \frac{16 - 15}{2}(362.78 + 393.69)\\ &= 1612.2 \text{ m} \end{split}\]
Learning Objectives
After successful completion of this lesson, you should be able to:
1) integrate functions given at discrete points by several methods.
Introduction
In a previous lesson, we used the trapezoidal rule with unequal segments to integrate a function given at discrete data points. In this lesson, we show other methods of integrating a function given at discrete data points. We do this through the same example as the previous lesson and skip the theory as you have already gone through it in previous lessons.
Example 1
The upward velocity of a rocket is given as a function of time in Table 1.
Table 1 Velocity as a function of time.
| \(t(\text{s})\) | \(v(t)(\text{m/s})\) |
|---|---|
| \(0\) | \(0\) |
| \(10\) | \(227.04\) |
| \(15\) | \(362.78\) |
| \(20\) | \(517.35\) |
| \(22.5\) | \(602.97\) |
| \(30\) | \(901.67\) |
Determine the distance \(s\) covered by the rocket from \(t = 11\ \text{s}\) to \(t = 16\ \text{s}\) using the velocity data provided and use any applicable numerical technique.
Solution
The distance covered \(s\) is given by
\[\int_{11}^{16} v{(t)}dt\]
Method: Average Function Method
The velocity of the rocket is not provided at \(t = 11\ \text{s}\) and \(t = 16\ \text{s},\) so we will have to use an interval that includes \(\left\lbrack 11,16 \right\rbrack\) to find the average velocity of the rocket within that domain. In this case, the interval \(\left\lbrack 10,20 \right\rbrack\) will suffice.
\[\begin{split} &v(10) = 227.04\\ &v(15) = 362.78\\ &v(20) = 517.35\end{split}\]
The average velocity, \(\bar{v}\) is
\[\begin{split} \bar{v} &= \frac{v(10) + v(15) + v(20)}{3}\\ &= \frac{227.04 + 362.78 + 517.35}{3}\\ &= 369.06\ \text{m/s} \end{split}\]
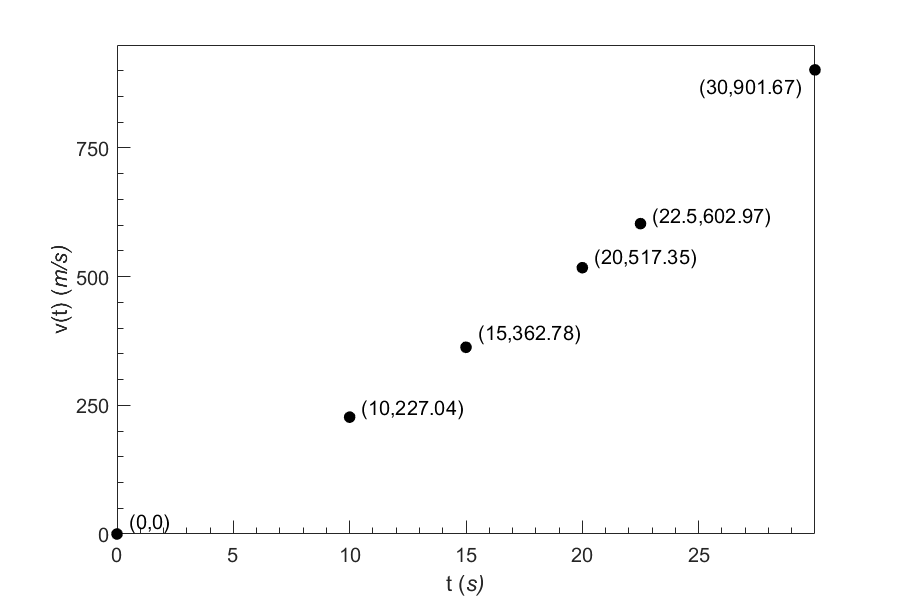
Figure 1 Velocity vs. time data for the rocket example
Using
\[s = \bar{v}\Delta t,\]
we get
\[\begin{split} s &= (369.06)(16 - 11)\\ &= 1845.3m \end{split}\]
As you see later, this method should NOT be used. Other methods that are as simple to use and to compute provide more accurate results. The average function method does not account for the differences in the individual segment widths and gives them equal consideration.
Method: Polynomial Interpolation Followed by Integration:
Because we are finding the area under the curve from \(\ t = 11\) to \(t = 16,\) we choose three points, \(t = 10,\) \(t = 15,\) and \(t = 20,\) to fit a quadratic polynomial through the data. Using polynomial interpolation, our resulting velocity function is (refer to Chapter 05.02 on direct (Vandermonde) method of interpolation)
\[v\left( t \right) = 12.05 + 17.733t + 0.3766t^{2},{\;\;}10 \leq t \leq 20.\]
Now, we simply take the integral of the quadratic within our limits, giving us
\[\begin{split} s &\approx \int_{11}^{16}{\left( 12.05 + 17.733t + 0.3766t^{2} \right){dt}}\\ &= \left\lbrack 12.05t + \frac{17.733t^{2}}{2} + \frac{0.3766t^{3}}{3} \right\rbrack_{11}^{16}\\ &= 12.05\left( 16 - 11 \right) + \frac{17.733}{2}\left( 16^{2} - 11^{2} \right) + \frac{0.3766}{3}\left( 16^{3} - 11^{3} \right)\\ &= 1604.3\ \text{m} \end{split}\]
Method: Spline Interpolation Followed by Integration
Fitting quadratic spline (refer to Chapter 05.05 on quadratic spline interpolation) through the data results in the following set of quadratics
\[\begin{split} v\left( t \right) &= - 0.15667t^{2} + 24.271t,\ 0 \leq t \leq 10\\ &= 1.2021t^{2} - 2.9053t + 135.88,\ 10 \leq t \leq 15\\ &= - 0.4489{3t}^{2} + 46.627t - 235.61,\ 15 \leq t \leq 20\\ &= 2.2315t^{2} - 60.589t + 836.55,\ 20 \leq t \leq 22.5\\ &= 39.827t - 293.13,\ 22.5 \leq t \leq 30 \end{split}\;\;\;\;\;\;\;\;\;\;\;\; (E1..16)\]
The value of the integral would then simply be
\[\begin{split} s &=\int_{11}^{16}v\left( t \right)dt\\ &= \int_{11}^{15}{v\left( t \right)dt + \int_{15}^{16}{v\left( t \right){dt}}} \end{split}\] Substituting proper quadratics based on the limits of integration gives
\[\begin{split} s &= \int_{11}^{15}{1.2021t^{2} - 2.9053t + 135.88\ dt}\\ &\ \ \ + \int_{15}^{16}{- 0.4489{3t}^{2} + 46.627t - 235.61dt}\\ &= \begin{bmatrix} \\ 1.2021\displaystyle\frac{t^{3}}{3} - 2.9053\displaystyle\frac{t^{2}}{2} + 135.88t \\ \\ \end{bmatrix}\begin{matrix} 15 \\ \\ 11 \\ \end{matrix}\\ &\ \ \ + \begin{bmatrix} \\ - 0.44893\displaystyle\frac{t^{3}}{3} + 46.627\frac{t^{2}}{2} - 235.61t \\ \\ \end{bmatrix}\begin{matrix} 16 \\ \\ 15 \\ \end{matrix}\\ &= 1211.49 + 379.22\\ &= 1590.7\ \text{m} \end{split}\]
Example 2
What is the absolute relative true error for each of the methods used in Example 1 if the data in Table 1 was obtained from the velocity profile,
\[v(t) = \left( 2000\ln\left\lbrack \frac{140000}{140000 - 2100t} \right\rbrack - 9.8t \right),\]
where \(v\) is given in m/s and \(t\) in s.
Solution
The exact distance covered between \(t =11\ \text{s}\) and \(t=16\ \text{s}\) is
\[\begin{split} s &= \int_{11}^{16}{\left( 2000\ln\left\lbrack \frac{140000}{140000 - 2100t} \right\rbrack - 9.8t \right){dt}}\\ &= 1604.9\ \text{m} \end{split}\]
Method: Average Function Method
The approximate value obtained using the average function method was \(1845.3\ \text{m}\). Hence, the absolute relative true error, \(\left| \epsilon_{t} \right|\), is
\[\begin{split} \left| \epsilon_{t} \right| &= \left| \frac{1604.9 - 1845.3}{1604.9} \right| \times 100\%\\ &= 14.976\% \end{split}\]
Method: Trapezoidal Rule with Unequal Segments
Although this method was illustrated in a previous lesson, we show it here for completion. The approximate value obtained using the trapezoidal rule with unequal segments was \(1612.2 \ \text{m}\). Hence, the absolute relative true error, \(\left| \epsilon_{t} \right|\), is
\[\begin{split} \left| \epsilon_{t} \right| &= \left| \frac{1604.9 - 1612.2}{1604.9} \right| \times 100\%\\ &= 0.451\% \end{split}\]
Method: Polynomial Interpolation Followed by Integration
The approximate value obtained using the direct polynomial was \(1604.3\ \text{m}\). Hence, the absolute relative true error, \(\left| \epsilon_{t} \right|\), is
\[\begin{split} \left| \epsilon_{t} \right| &= \left| \frac{1604.9 - 1604.3}{1604.9} \right| \times 100\%\\ &= 0.037\% \end{split}\]
Method: Spline Interpolation Followed by Integration
The approximate value obtained using the spline interpolation was \(1595.9\ \text{m}.\) Hence, the absolute relative true error, \(\left| \epsilon_{t} \right|\), is
\[\begin{split} \left| \epsilon_{t} \right| &= \left| \frac{1604.9 - 1590.7}{1604.9} \right| \times 100\%\\ &= 0.885\% \end{split}\]
Table 2 Comparison of numerical integration methods for functions given at discrete data points.
| Method | Approximate Value (m) | \(\left|{\epsilon_{t }}\right|\) |
|---|---|---|
| Average Function | \(1845.3\) | \(14.976\%\) |
| Trapezoidal Rule | \(1612.2\) | \(0.451\%\) |
| Polynomial Interpolation | \(1604.3\) | \(0.037\%\) |
| Spline Interpolation | \(1595.9\) | \(0.885\%\) |
The values of the absolute relative true error in Table 2 should be a reason to question the use of the average function method. The trapezoidal rule which is equally simple to apply results in much less true error.
Multiple Choice Test
(1). Given below is the discrete data of \(y\) vs \(x\).
| \(x\) | \(0\) | \(10\) | \(15\) | \(20\) |
|---|---|---|---|---|
| \(y\) | \(100.00\) | \(227.04\) | \(362.78\) | \(517.35\) |
Amongst the following methods, which one would be the best scientific method to use to find the integral \(\displaystyle \int_{0}^{20}{ydx}\)?
(A) Average function method
(B) Trapezoidal rule with unequal segments
(C) \(y\left( 10 \right) \times \left( 20 \right)\)
(D) \(y\left( 20 \right) \times 20\)
(2). Given \((x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})\) data pairs where\(\ x_{1} < x_{2} < x_{3}\), then \(\displaystyle \int_{x_{1}}^{x_{3}}{y(x)dx}\) can be best approximated as
(A) \(\displaystyle \frac{y_{1} + y_{2} + y_{3}}{3}(x_{3} - x_{1})\)
(B) \(\displaystyle \frac{y_{1} + y_{2}}{2}(x_{3} - x_{1})\)
(C) \(\displaystyle (x_{2} - x_{1})(\frac{y_{1} + y_{2}}{2}) + (x_{3} - x_{2})(\frac{y_{2} + y_{3}}{2})\)
(D) \(\displaystyle y_{2}(x_{3} - x_{1})\)
(3). The following data of the velocity of a body as a function of time is given.
| \(\text{Time},\ t\ (s)\) | \(0\) | \(15\) | \(18\) | \(22\) | \(24\) |
|---|---|---|---|---|---|
| \(\text{Velocity},\ v\ (m/s)\) | \(22\) | \(24\) | \(31.4\) | \(25\) | \(123\) |
Using the trapezoidal rule with unequal segments, the distance covered in meters by the body from \(t\)=\(15\) to \(22\ s\) is
(A) \(171.5\)
(B) \(187.6\)
(C) \(195.9\)
(D) \(204.9\)
(4). The following data of the velocity of a body as a function of time is given.
| \(\text{Time},\ t\ (s)\) | \(0\) | \(15\) | \(18\) | \(22\) | \(24\) |
|---|---|---|---|---|---|
| \(\text{Velocity},\ v\ (m/s)\) | \(22\) | \(24\) | \(37\) | \(25\) | \(123\) |
Using the trapezoidal rule with unequal segments, the distance covered in meters by the body from \(t\)=\(9.3\) to \(18\ s\) is
(A) \(226.1\)
(B) \(240.7\)
(C) \(262.0\)
(D) \(436.5\)
(5). The flow rate of oil is given in gallons per hour through a pipeline over a 12-hour period as shown.
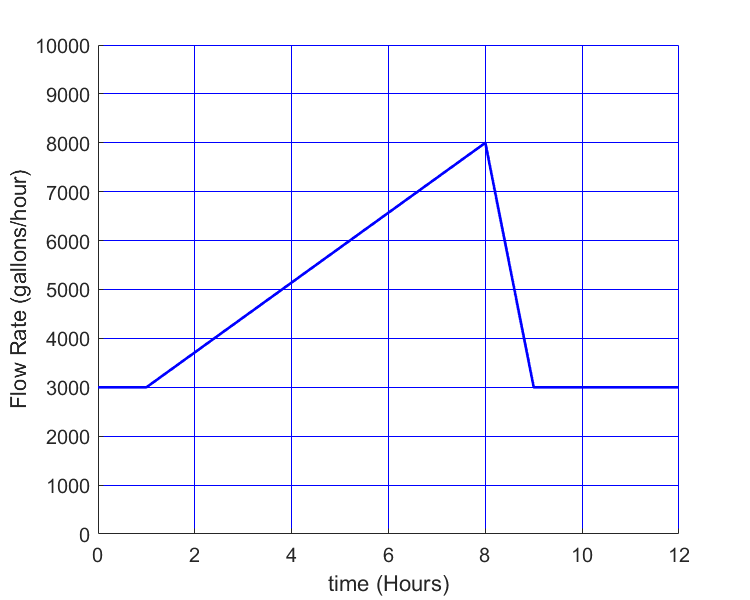
The best approximation of the number of gallons of oil that has flowed through the 12-hour period is
(A) \(48000\)
(B) \(56000\)
(C) \(66000\)
(D) \(86148\)
(6). Water is flowing through a circular pipe of 0.5 ft radius, and flow velocity (ft/s) measurements are made from the center to the wall of the pipe as follows.
\(\text{Radial Location},\) \(r\) (\(ft\)) |
\(0\) | \(0.17\) | \(0.33\) | \(0.50\) |
|---|---|---|---|---|
\(\text{Velocity},\) \(v\) (\(ft/s\)) |
\(10\) | \(8.8\) | \(5.6\) | \(0\) |
Note that the volumetric flow rate, \(\dot{Q}\) is given by
\[\displaystyle \dot{Q} = \int_{0}^{a}{2\pi rv(r)dr}\]
where \(v(r)\) is the flow velocity of the fluid as a function of the radial location, \(r\), and \(a\) is the radius of the pipe. The volumetric flow rate in \(ft^{3}/s\) in the pipe by using trapezoidal rule with unequal segments is
(A) \(3.226\)
(B) \(3.469\)
(C) \(3.901\)
(D) \(20.27\)
For complete solution, go to
http://nm.mathforcollege.com/mcquizzes/07int/quiz_07int_discrete_solution.pdf
Problem Set
(1). The following data of the velocity of a body as a function of time is given.
| \(\text{Time}\ (s)\) | \(0\) | \(15\) | \(18\) | \(22\) | \(24\) |
|---|---|---|---|---|---|
| \(\text{Velocity}\ ({m}/{s})\) | \(22\) | \(24\) | \(37\) | \(25\) | \(123\) |
Use trapezoidal rule with unequal segments OR a better scientific method to find the displacement of the body from \(t = 15\) to \(22\) seconds.
Answer: \(215.5\ m\)
(2). The following data of the velocity of a body as a function of time is given.
| \(\text{Time}\ (s)\) | \(0\) | \(15\) | \(18\) | \(22\) | \(24\) |
|---|---|---|---|---|---|
| \(\text{Velocity}\ ({m}/{s})\) | \(22\) | \(24\) | \(37\) | \(25\) | \(123\) |
Use trapezoidal rule with unequal segments OR a better scientific method to find the displacement of the body from \(t = 13\) to \(18\) seconds.
Answer: \(139.23\ m\) by trapezoidal rule with unequal segments
(3). Water is flowing out at the end of 20 meter long U-shaped channel and falls into a field at the flow rate given below as a function of time.
| \(\text{Time}\ (s)\) | \(2\) | \(4\) | \(7\) | \(10\) |
|---|---|---|---|---|
| \(\text{Flow rate}\ ({m^{3}}/{s})\) | \(12\) | \(15\) | \(17\) | \(14\) |
Use trapezoidal rule for discrete data to find the amount of water that fell on the field between \(t = 3\) and \(t = 9\)seconds.
Answer: \(94.25\ m^3\)
(4). Water is flowing out at the end of 20 meter long U-shaped channel and falls into a field at the flow rate given below as a function of time.
| \(\text{Time}\ (s)\) | \(2\) | \(4\) | \(7\) | \(10\) |
|---|---|---|---|---|
| \(\text{Flow rate} ({m^{3}}/{s})\) | \(12\) | \(15\) | \(17\) | \(14\) |
Use Simpson’s 1/3 rule to find the amount of water that fell on the field between \(t = 4\) and \(t = 10\) seconds.
Answer: \(97 \ m^3\)
(5). Water is flowing through a circular pipe of 1/2 ft radius and flow velocity (ft/s) measurements are made from the center to the wall of the pipe as follows
| \(\text{Radial Location,}\ r\ (\text{ft})\) | \(0\) | \(0.083\) | \(0.17\) | \(0.25\) | \(0.33\) | \(0.42\) | \(0.50\) |
|---|---|---|---|---|---|---|---|
| \(\text{Velocity,}\ v ({\text{ft}}/{s})\) | \(10\) | \(9.72\) | \(8.88\) | \(7.5\) | \(5.6\) | \(3.1\) | \(0\) |
Estimate the flow rate in the pipe.
Answer: \(3.8477 ft^3/s\) by trapezoidal rule with unequal segments
(6). Below is the data given for thermal expansion coefficient of steel as a function of temperature.
| Temperature | Instantaneous thermal expansion coefficient | ||
|---|---|---|---|
| \(^\circ F\) | \(^\circ C\) | \(K\) | \((\mu{\text{in}}/ {{\text{in}}/{^\circ F}})\) |
| \(80\) | \(26.67\) | \(299.67\) | \(6.47\) |
| \(60\) | \(15.56\) | \(288.56\) | \(6.36\) |
| \(40\) | \(4.44\) | \(277.44\) | \(6.24\) |
| \(20\) | \(-6.67\) | \(266.33\) | \(6.12\) |
| \(0\) | \(-17.78\) | \(255.22\) | \(6.00\) |
| \(-20\) | \(-28.89\) | \(244.11\) | \(5.86\) |
| \(-40\) | \(-40.00\) | \(233.00\) | \(5.72\) |
| \(-60\) | \(-51.11\) | \(221.89\) | \(5.58\) |
| \(-80\) | \(-62.22\) | \(210.78\) | \(5.43\) |
| \(-100\) | \(-73.33\) | \(199.67\) | \(5.28\) |
| \(-120\) | \(-84.44\) | \(188.56\) | \(5.09\) |
| \(-140\) | \(-95.56\) | \(177.44\) | \(4.91\) |
| \(-160\) | \(-106.67\) | \(166.33\) | \(4.72\) |
| \(-180\) | \(-117.78\) | \(155.22\) | \(4.52\) |
| \(-200\) | \(-128.89\) | \(144.11\) | \(4.30\) |
| \(-220\) | \(-140.00\) | \(133.00\) | \(4.08\) |
| \(-240\) | \(-151.11\) | \(121.89\) | \(3.83\) |
| \(-260\) | \(-162.22\) | \(110.78\) | \(3.58\) |
| \(-280\) | \(-173.33\) | \(99.67\) | \(3.33\) |
| \(-300\) | \(-184.44\) | \(88.56\) | \(3.07\) |
| \(-320\) | \(-195.56\) | \(77.44\) | \(2.76\) |
| \(-340\) | \(-206.67\) | \(66.33\) | \(2.45\) |
A bascule bridge designer needs to shrink fit a solid circular shaft \(A\) of diameter \(12.363^{\prime\prime}\) in a hollow cylinder \(B\) with inner diameter \(12.358^{\prime\prime}\). His plan is to put the solid shaft \(A\) in dry-ice/alcohol mixture to contract its diameter so that it can be slid through the inner diameter of cylinder \(B\). He also needs a diametral clearance of at least \(0.01^{\prime\prime}\) so that the shafts do not touch each other before the whole shaft \(A\) is slid through. Assume the room temperature is \(70^{\circ}F\) and the dry-ice/alcohol mixture is \(- 108^{\circ}F\). Solve the following problems.
a) A consultant on this project assumed the thermal expansion coefficient is constant over the temperature range. He used the value of thermal expansion coefficient at \(80^{\circ}F\) in all his calculations. Find the contraction of diameter in the shaft\(A\).
b) In part (a), does he calculate enough contraction in the shaft \(A\) diameter?
c) Is his assumption of assuming constant thermal expansion correct? Why or why not? A single sentence answer will do.
d) How would you solve the problem? Solve by at least two different methods you learned in class. Do you calculate enough contraction in shaft \(A\) diameter?
e) If you did not get enough contraction in the diameter in part (d), what would you suggest? Give a quantified solution, not just a qualitative answer.
Answer: \(a)\ -0.14238^{\prime\prime}\)
\(b)\) No, needed contraction is \(0.015^{\prime\prime}\)
\(c)\) Not a good assumption as the coefficient of thermal expansion is a function of temperature.
\(d)\) trapezoidal rule with unequal segments=\(-0.12872^{\prime\prime}\); polynomial regression=\(-0.012897^{\prime\prime}\)
\(e)\) cool in liquid nitrogen; you will get an estimated contraction of \(-0.023627^{\prime\prime}\)