Chapter 04.10: Eigenvalues and Eigenvectors
Learning Objectives
After successful completion, you should be able to:
1) define eigenvalues and eigenvectors of a square matrix,
2) find eigenvalues and eigenvectors of a square matrix,
3) relate eigenvalues to the singularity of a square matrix, and
4) use the power method to numerically find the largest eigenvalue in magnitude of a square matrix and the corresponding eigenvector.
What does eigenvalue mean?
The word eigenvalue comes from the German word Eigenwert where Eigen means characteristic and Wert means value. However, what the word means is not on your mind! You want to know why I need to learn about eigenvalues and eigenvectors. Once I give you an example of an application of eigenvalues and eigenvectors, you will want to know how to find these eigenvalues and eigenvectors.
Can you give me a physical example application of eigenvalues and eigenvectors?
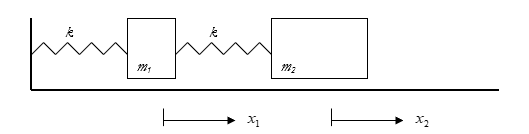
Look at the spring-mass system as shown in the picture below.
Assume each of the two mass-displacements to be denoted by \(x_{1}\) and \(x_{2}\), and let us assume each spring has the same spring constant \(k\). Then by applying Newton’s 2nd and 3rd law of motion to develop a force-balance for each mass we have
\[m_{1}\frac{d^{2}x_{1}}{dt^{2}} = - kx_{1} + k(x_{2} - x_{1})\]
\[m_{2}\frac{d^{2}x_{2}}{dt^{2}} = - k(x_{2} - x_{1})\]
Rewriting the equations, we have
\[m_{1}\frac{d^{2}x_{1}}{dt^{2}} - k( - 2x_{1} + x_{2}) = 0\]
\[m_{2}\frac{d^{2}x_{2}}{dt^{2}} - k(x_{1} - x_{2}) = 0\]
Let \(m_{1}\ = 10,\ m_{2} = 20,k = 15\)
\[10\frac{d^{2}x_{1}}{dt^{2}} - 15( - 2x_{1} + x_{2}) = 0\]
\[20\frac{d^{2}x_{2}}{dt^{2}} - 15(x_{1} - x_{2}) = 0\]
From vibration theory, the solutions can be of the form
\[x_{i} = A_{i}\sin\left( \omega t - \Theta \right)\]
where
\(A_{i}\)= amplitude of the vibration of mass \(i\),
\(\omega\) = frequency of vibration,
\(\Theta\) = phase shift.
then
\[\frac{d^{2}x_{i}}{dt^{2}} = - A_{i}w^{2}{Sin}(\omega t - \Theta)\]
Substituting \(x_{i}\)and \(\frac{d^{2}x_{i}}{dt^{2}}\)in equations,
\[- 10A_{1}\omega^{2} - 15( - 2A_{1} + A_{2}) = 0\]
\[- 20A_{2}\omega^{2} - 15(A_{1} - A_{2}) = 0\]
gives
\[( - 10\omega^{2} + 30)A_{1} - 15A_{2} = 0\]
\[- 15A_{1} + ( - 20\omega^{2} + 15)A_{2} = 0\]
or
\[( - \omega^{2} + 3)A_{1} - 1.5A_{2} = 0\]
\[- 0.75A_{1} + ( - \omega^{2} + 0.75)A_{2} = 0\]
In matrix form, these equations can be rewritten as
\[\begin{bmatrix} - \omega^{2} + 3 & - 1.5 \\ - 0.75 & - \omega^{2} + 0.75 \\ \end{bmatrix}\begin{bmatrix} A_{1} \\ A_{2} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix}\]
\[\begin{bmatrix} 3 & - 1.5 \\ - 0.75 & 0.75 \\ \end{bmatrix}\begin{bmatrix} A_{1} \\ A_{2} \\ \end{bmatrix} - \omega^{2}\begin{bmatrix} A_{1} \\ A_{2} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix}\]
Let \(\omega^{2} = \lambda\)
\[\lbrack A\rbrack = \begin{bmatrix} 3 & - 1.5 \\ - 0.75 & 0.75 \\ \end{bmatrix}\]
\[\lbrack X\rbrack = \begin{bmatrix} A_{1} \\ A_{2} \\ \end{bmatrix}\]
\[\lbrack A\rbrack\ \lbrack X\rbrack - \lambda\lbrack X\rbrack = 0\]
\[\lbrack A\rbrack\ \lbrack X\rbrack = \lambda\lbrack X\rbrack\]
In the above equation, \(\lambda\) is the eigenvalue and \(\lbrack X\rbrack\) is the eigenvector corresponding to \(\lambda\). As you can see, if we know \(\lambda\) for the above example we can calculate the natural frequency of the vibration
\(\omega = \sqrt{\lambda}\)
Why are the natural frequencies of vibration important? Because you do not want to have a forcing force on the spring-mass system close to this frequency as it would make the amplitude \(A_{i}\) very large and make the system unstable.
What is the general definition of eigenvalues and eigenvectors of a square matrix?
If \(\lbrack A\rbrack\) is a \(n \times n\) matrix, then \(\lbrack X\rbrack \neq \overrightarrow{0}\) is an eigenvector of \(\lbrack A\rbrack\) if
\[\lbrack A\rbrack\ \lbrack X\rbrack = \lambda\lbrack X\rbrack\]
where \(\lambda\) is a scalar and \(\lbrack X\rbrack \neq 0\). The scalar \(\lambda\) is called the eigenvalue of \(\lbrack A\rbrack\)and \(\lbrack X\rbrack\) is called the eigenvector corresponding to the eigenvalue\(\lambda\).
How do I find eigenvalues of a square matrix?
To find the eigenvalues of a \(n \times n\) matrix \(\lbrack A\rbrack\ \), we have
\[\lbrack A\rbrack\ \lbrack X\rbrack = \lambda\lbrack X\rbrack\]
\[\lbrack A\rbrack\ \lbrack X\rbrack - \lambda\lbrack X\rbrack = 0\]
\[\lbrack A\rbrack\ \lbrack X\rbrack - \lambda\ \lbrack I\rbrack\lbrack X\rbrack = 0\]
\[(\lbrack A\rbrack\ - \lbrack\lambda\rbrack\lbrack I\rbrack)\lbrack X\rbrack = 0\]
Now for the above set of equations to have a nonzero solution,
\[det(\lbrack A\rbrack - \lambda\lbrack I\rbrack) = 0\]
This left-hand side can be expanded to give a polynomial in \(\lambda\) and solving the above equation would give us values of the eigenvalues. The above equation is called the characteristic equation of \(\lbrack A\rbrack\).
For a \(\lbrack A\rbrack\) \(n \times n\) matrix, the characteristic polynomial of \(A\) is of degree \(n\) as follows
\[det(\lbrack A\rbrack - \lambda\lbrack I\rbrack) = 0\]
giving
\[\lambda^{n} + c_{1}\lambda^{n - 1} + c_{2}\lambda^{n - 2} + - - + c_{n} = 0\]
Hence. this polynomial has \(n\) roots.
Example 1
Find the eigenvalues of the physical problem discussed in the beginning of this chapter, that is, find the eigenvalues of the matrix
\[\lbrack A\rbrack = \begin{bmatrix} 3 & - 1.5 \\ - 0.75 & 0.75 \\ \end{bmatrix}\]
Solution
\[\lbrack A\rbrack - \lambda\lbrack I\rbrack = \begin{bmatrix} 3 - \lambda & - 1.5 \\ - 0.75 & 0.75 - \lambda \\ \end{bmatrix}\]
\[det(\left\lbrack A \right\rbrack - \lambda\left\lbrack I \right\rbrack) = (3 - \lambda)(0.75 - \lambda) - ( - 0.75)( - 1.5) = 0\]
\[2.25 - 0.75\lambda - 3\lambda + \lambda^{2} - 1.125 = 0\]
\[\lambda^{2} - 3.75\lambda + 1.125 = 0\]
\[\begin{split} \lambda &= \frac{- ( - 3.75) \pm \sqrt{( - 3.75)^{2} - 4(1)(1.125)}}{2(1)}\\ &= \frac{3.75 \pm 3.092}{2}\\ &= 3.421,\ 0.3288 \end{split}\]
So the eigenvalues are \(3.421\) and \(0.3288\).
Example 2
Find the eigenvectors of
\[A = \begin{bmatrix} 3 & - 1.5 \\ - 0.75 & 0.75 \\ \end{bmatrix}\]
Solution
The eigenvalues have already been found in Example 1 as
\[\lambda_{1} = 3.421,\lambda_{2} = 0.3288\]
Let
\[\lbrack X\rbrack = \begin{bmatrix} x_{1} \\ x_{2} \\ \end{bmatrix}\]
be the eigenvector corresponding to
\[\lambda_{1} = 3.421\]
Hence
\[(\lbrack A\rbrack - \lambda_{1}\lbrack I\rbrack)\lbrack X\rbrack = 0\]
\[\left\{ \begin{bmatrix} 3 & - 1.5 \\ - 0.75 & 0.75 \\ \end{bmatrix} - 3.421\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \right\}\begin{bmatrix} x_{1} \\ x_{2} \\ \end{bmatrix} = 0\]
\[\begin{bmatrix} - 0.421 & - 1.5 \\ - 0.75 & - 2.671 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix}\]
If
\[x_{1} = s\]
then
\[\begin{matrix} - 0.421s - 1.5x_{2} = 0 \\ x_{2} = - 0.2808s \\ \end{matrix}\]
The eigenvector corresponding to \(\lambda_{1} = 3.421\) then is
\[\begin{split} \lbrack X\rbrack &= \begin{bmatrix} s \\ - 0.2808s \\ \end{bmatrix}\\ &= s\begin{bmatrix} 1 \\ - 0.2808 \\ \end{bmatrix} \end{split}\]
The eigenvector corresponding to
\[\lambda_{1} = 3.421\]
is
\[\begin{bmatrix} 1 \\ - 0.2808 \\ \end{bmatrix}\]
Similarly, the eigenvector corresponding to
\[\lambda_{2} = 0.3288\]
is
\[\begin{bmatrix} 1 \\ 1.781 \\ \end{bmatrix}\]
Example 3
Find the eigenvalues and eigenvectors of
\[\lbrack A\rbrack = \begin{bmatrix} 1.5 & 0 & 1 \\ - 0.5 & 0.5 & - 0.5 \\ - 0.5 & 0 & 0 \\ \end{bmatrix}\]
Solution
The characteristic equation is given by
\[det(\lbrack A\rbrack - \lambda\lbrack I\rbrack) = 0\]
\[\det\begin{bmatrix} 1.5 - \lambda & 0 & 1 \\ - 0.5 & 0.5 - \lambda & - 0.5 \\ - 0.5 & 0 & - \lambda \\ \end{bmatrix} = 0\]
\[(1.5 - \lambda)\lbrack(0.5 - \lambda)( - \lambda) - ( - 0.5)(0)\rbrack + (1)\lbrack( - 0.5)(0) - ( - 0.5)(0.5 - \lambda)\rbrack = 0\]
\[- \lambda^{3} + 2\lambda^{2} - 1.25\lambda + 0.25 = 0\]
To find the roots of the characteristic polynomial equation
\[- \lambda^{3} + 2\lambda^{2} - 1.25\lambda + 0.25 = 0\]
we find that the first root by observation is
\[\lambda = 1\]
as substitution of \(\lambda = 1\)gives
\[( - 1)^{3} + 2(1)^{2} - 1.25(1) + 0.25 = 0\] \[0= 0\]
So
\[(\lambda - 1)\]
is a factor of
\[- \lambda^{3} + 2\lambda^{2} - 1.25\lambda + 0.25\]
To find the other factors of the characteristic polynomial, we first conduct long division
\[- \lambda^{2} + \lambda + 0.25\]
\[\left( \ \lambda - 1 \right)\overline{- \lambda^{3} + 2\lambda^{2} - 1.25\lambda + 0.25}\]
\[- \lambda^{3} + \lambda^{2}\]
\[\overline{\lambda^{2} - 1.25\lambda + 0.25}\]
\[\lambda^{2} - \lambda\]
\[\overline{- 0.25\lambda + 0.25}\]
\[\overline{- 0.25\lambda + 0.25}\]
Hence
\[- \lambda^{3} + 2\lambda^{2} - 1.25\lambda + 0.25 = (\lambda - 1)( - \lambda^{2} + \lambda + 0.25)\]
To find zeroes of\(- \lambda^{2} + \lambda + 0.25\), we solve the quadratic equation,
\[- \lambda^{2} + \lambda + 0.25 = 0\]
to give
\[\begin{split} \lambda &=\frac{-(1) \pm \sqrt{(1)^2-(4)(-1)(0.25)}}{2(-1)}\\ &= \frac{- 1 \pm \sqrt{0}}{- 2}\\ &= 0.5,0.5 \end{split}\]
So \ \(\lambda = 0.5\) and \(\lambda = 0.5\) are the zeroes of
\[- \lambda^{2} + \lambda + 0.5\]
giving
\[- \lambda^{2} + \lambda + 0.25 = - (\lambda - 0.5)(\lambda - 0.5)\]
Hence
\[- \lambda^{3} + 2\lambda^{2} - 1.25\lambda + 0.25 = 0\]
can be rewritten as
\[- (\lambda - 1)(\lambda - 0.5)(\lambda - 0.5) = 0\]
to give the roots as
\[\lambda = 1,\ \ 0.5,\ \ 0.5\]
These are the three roots of the characteristic polynomial equation and hence the eigenvalues of matrix [A].
Note that there are eigenvalues that are repeated. Since there are only two distinct eigenvalues, there are only two eigenspaces. But, corresponding to \(\lambda = 0.5\) there should be two eigenvectors that form a basis for the eigenspace corresponding to \(\lambda = 0.5\).
Given
\[\lbrack(A - \lambda I)\rbrack\ \lbrack X\rbrack = 0\]
then
\[\begin{bmatrix} 1.5 - \lambda & 0 & 1 \\ - 0.5 & 0.5 - \lambda & - 0.5 \\ - 0.5 & 0 & - \lambda \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \end{bmatrix}\]
For \(\lambda = 0.5\),
\[\begin{bmatrix} 1 & 0 & 1 \\ - 0.5 & 0 & - 0.5 \\ - 0.5 & 0 & - 0.5 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \end{bmatrix}\]
Solving this system gives
\[x_{1} = - a,\ x_{2} = b,\ x_{3} = a\]
So
\[\begin{split} \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} &= \begin{bmatrix} - a \\ b \\ a \\ \end{bmatrix}\\ & = \begin{bmatrix} - a \\ 0 \\ a \\ \end{bmatrix} + \begin{bmatrix} 0 \\ b \\ 0 \\ \end{bmatrix}\\ &= a\begin{bmatrix} - 1 \\ 0 \\ 1 \\ \end{bmatrix} + b\begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix} \end{split}\]
So, the vectors \(\begin{bmatrix} - 1 \\ 0 \\ 1 \\ \end{bmatrix}\) and \(\begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix}\) form a basis for the eigenspace for the eigenvalue \(\lambda = 0.5\) and are the two eigenvectors corresponding to \(\lambda = 0.5\).
For \(\lambda = 1\),
\[\begin{bmatrix} 0.5 & 0 & 1 \\ - 0.5 & - 0.5 & - 0.5 \\ - 0.5 & 0 & - 1 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \end{bmatrix}\]
Solving this system gives
\[x_{1} = a,\ x_{2} = - 0.5a,\ x_{3} = - 0.5a\]
The eigenvector corresponding to \(\lambda = 1\) is
\[\begin{bmatrix} a \\ - 0.5a \\ - 0.5a \\ \end{bmatrix} = a\begin{bmatrix} 1 \\ - 0.5 \\ - 0.5 \\ \end{bmatrix}\]
Hence the vector
\[\begin{bmatrix} 1 \\ - 0.5 \\ - 0.5 \\ \end{bmatrix}\]
is a basis for the eigenspace for the eigenvalue of\(\lambda = 1\), and is the eigenvector corresponding to \(\lambda = 1\).
What are some of the theorems of eigenvalues and eigenvectors?
Theorem 1: If \(\lbrack A\rbrack\) is a \(n \times n\) triangular matrix – upper triangular, lower triangular or diagonal, the eigenvalues of \(\lbrack A\rbrack\) are the diagonal entries of\(\lbrack A\rbrack\).
Theorem 2: \(\lambda = 0\) is an eigenvalue of \(\lbrack A\rbrack\) if \(\lbrack A\rbrack\) is a singular (noninvertible) matrix.
Theorem 3: \(\lbrack A\rbrack\) and \(\lbrack A\rbrack^{T}\) have the same eigenvalues.
Theorem 4: Eigenvalues of a symmetric matrix are real.
Theorem 5: Eigenvectors of a symmetric matrix are orthogonal, but only for distinct eigenvalues.
Theorem 6: \(\left| det(A) \right|\) is the product of the absolute values of the eigenvalues of\(\lbrack A\rbrack\).
Example 4
What are the eigenvalues of
\[\lbrack A\rbrack = \begin{bmatrix} 6 & 0 & 0 & 0 \\ 7 & 3 & 0 & 0 \\ 9 & 5 & 7.5 & 0 \\ 2 & 6 & 0 & - 7.2 \\ \end{bmatrix}\]
Solution
Since the matrix \(\lbrack A\rbrack\) is a lower triangular matrix, the eigenvalues of \(\lbrack A\rbrack\) are the diagonal elements of\(\lbrack A\rbrack\). The eigenvalues are
\[\lambda_{1} = 6,\ \lambda_{2} = 3,\ \lambda_{3} = 7.5,\ \lambda_{4} = - 7.2\]
Example 5
One of the eigenvalues of
\[\ \lbrack A\rbrack = \begin{bmatrix} 5 & 6 & 2 \\ 3 & 5 & 9 \\ 2 & 1 & - 7 \\ \end{bmatrix}\]
is zero. Is \(\lbrack A\rbrack\) invertible?
Solution
\(\lambda = 0\) is an eigenvalue of \(\lbrack A\rbrack\), that implies \(\lbrack A\rbrack\) is singular and is not invertible.
Example 6
Given the eigenvalues of
\[\lbrack A\rbrack = \begin{bmatrix} 2 & - 3.5 & 6 \\ 3.5 & 5 & 2 \\ 8 & 1 & 8.5 \\ \end{bmatrix}\]
are
\[\lambda_{1} = - 1.547,\ \lambda_{2} = 12.33,\ \lambda_{3} = 4.711\]
What are the eigenvalues of \(\lbrack B\rbrack\) if
\[\lbrack B\rbrack = \begin{bmatrix} 2 & 3.5 & 8 \\ - 3.5 & 5 & 1 \\ 6 & 2 & 8.5 \\ \end{bmatrix}\]
Solution
Since \(\lbrack B\rbrack = \lbrack A\rbrack^{T}\), the eigenvalues of \(\lbrack A\rbrack\) and \(\lbrack B\rbrack\) are the same. Hence eigenvalues of \(\lbrack B\rbrack\) also are
\[\lambda_{1} = - 1.547,\ \lambda_{2} = 12.33,\ \lambda_{3} = 4.711\]
Example 7
Given the eigenvalues of
\[\lbrack A\rbrack = \begin{bmatrix} 2 & - 3.5 & 6 \\ 3.5 & 5 & 2 \\ 8 & 1 & 8.5 \\ \end{bmatrix}\]
are
\[\lambda_{1} = - 1.547,\ \lambda_{2} = 12.33,\ \lambda_{3} = 4.711\]
Calculate the magnitude of the determinant of the matrix.
Solution
Since
\[\begin{split} \left| det\lbrack A\rbrack \right| &= \left| \lambda_{1} \right|\ \left| \lambda_{2} \right|\ \left| \lambda_{3} \right|\\ &= \left| - 1.547 \right|\ \left| 12.33 \right|\ \left| 4.711 \right|\\ &= 89.88 \end{split}\]
How does one find eigenvalues and eigenvectors numerically?
One of the most common methods used for finding eigenvalues and eigenvectors is the power method. It is used to find the largest eigenvalue in an absolute sense. Note that if this largest eigenvalues is repeated, this method will not work. Also this eigenvalue needs to be distinct. The method is as follows:
(1). Assume a guess \(\lbrack X^{(0)}\rbrack\) for the eigenvector in
\[\lbrack A\rbrack\ \lbrack X\rbrack = \lambda\lbrack X\rbrack\]
equation. One of the entries of \(\lbrack X^{(0)}\rbrack\) needs to be unity.
(2). Find
\[\lbrack Y^{(1)}\rbrack = \lbrack A\rbrack\ \lbrack X^{(0)}\rbrack\]
(3). Scale \(\lbrack Y^{(1)}\rbrack\) so that the chosen unity component remains unity.
\[\lbrack Y^{(1)}\rbrack = \lambda^{(1)}\lbrack X^{(1)}\rbrack\]
(4). Repeat steps (2) and (3) with
\(\lbrack X\rbrack = \lbrack X^{(1)}\rbrack\) to get \(\lbrack X^{(2)}\rbrack\).
(5). Repeat the steps 2 and 3 until the value of the eigenvalue converges.
If \(E_{s}\)is the pre-specified percentage relative error tolerance to which you would like the answer to converge to, keep iterating until
\[\left| \frac{\lambda^{(i + 1)} - \lambda^{(i)}}{\lambda^{(i + 1)}} \right| \times 100 \leq E_{s}\]
where the left-hand side of the above inequality is the definition of absolute percentage relative approximate error, denoted generally by\(E_{s}\) A pre-specified percentage relative tolerance of \(0.5 \times 10^{2 - m}\) implies at least \(m\) significant digits are current in your answer. When the system converges, the value of \(\lambda\) is the largest (in absolute value) eigenvalue of \(\lbrack A\rbrack\).
Example 8
Using the power method, find the largest eigenvalue and the corresponding eigenvector of
\[\lbrack A\rbrack = \begin{bmatrix} 1.5 & 0 & 1 \\ - 0.5 & 0.5 & - 0.5 \\ - 0.5 & 0 & 0 \\ \end{bmatrix}\]
Solution
Assume
\[\lbrack X^{(0)}\rbrack = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix}\]
\[\begin{split} \lbrack A\rbrack\ \lbrack X^{(0)}\rbrack &= \begin{bmatrix} 1.5 & 0 & 1 \\ - 0.5 & 0.5 & - 0.5 \\ - 0.5 & 0 & 0 \\ \end{bmatrix}\begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix}\\ &= \begin{bmatrix} 2.5 \\ - 0.5 \\ - 0.5 \\ \end{bmatrix} \end{split}\]
\[Y^{(1)} = 2.5\begin{bmatrix} 1 \\ - 0.2 \\ - 0.2 \\ \end{bmatrix}\]
\[\lambda^{(1)} = 2.5\]
We will choose the first element of \(\lbrack X^{(0)}\rbrack\) to be unity.
\[\lbrack X^{(1)}\rbrack = \begin{bmatrix} 1 \\ - 0.2 \\ - 0.2 \\ \end{bmatrix}\]
\[\begin{split} \lbrack A\rbrack\ \lbrack X^{(1)}\rbrack &= \begin{bmatrix} 1.5 & 0 & 1 \\ - 0.5 & 0.5 & - 0.5 \\ - 0.5 & 0 & 0 \\ \end{bmatrix}\begin{bmatrix} 1 \\ - 0.2 \\ - 0.2 \\ \end{bmatrix}\\ &= \begin{bmatrix} 1.3 \\ - 0.5 \\ - 0.5 \\ \end{bmatrix} \end{split}\]
\[\lbrack X^{(2)}\rbrack = 1.3\begin{bmatrix} 1 \\ - 0.3846 \\ - 0.3846 \\ \end{bmatrix}\]
\[\lambda^{(2)} = 1.3\]
\[\lbrack X^{(2)}\rbrack = \begin{bmatrix} 1 \\ - 0.3846 \\ - 0.3846 \\ \end{bmatrix}\]
The absolute relative approximate error in the eigenvalues is
\[\begin{split} \left| \varepsilon_{a} \right| &= \left| \frac{\lambda^{(2)} - \lambda^{(1)}}{\lambda^{(2)}} \right| \times 100\\ &= \left| \frac{1.3 - 1.5}{1.5} \right| \times 100\\ &= 92.307\% \end{split}\]
Conducting further iterations, the values of \(\lambda^{(i)}\)and the corresponding eigenvectors is given in the table below
| \(i\) | \(\lambda^{(i)}\) | \(\lbrack X^{(i)}\rbrack\) | \(\left| \varepsilon_{a} \right|\ \ (\%)\) |
|---|---|---|---|
| \(1\) | \(2.5\) | \[\begin{bmatrix} 1 \\ - 0.2 \\ - 0.2 \\\end{bmatrix}\] | _____ |
| \(2\) | \(1.3\) | \[\begin{bmatrix} 1 \\ - 0.38462 \\ - 0.38462 \\\end{bmatrix}\] | \(92.307\) |
| \(3\) | \(1.1154\) | \[\begin{bmatrix} 1 \\ - 0.44827 \\ - 0.44827 \\\end{bmatrix}\] | \(16.552\) |
| \(4\) | \(1.0517\) | \[\begin{bmatrix} 1 \\ - 0.47541 \\ - 0.47541 \\\end{bmatrix}\] | \(6.0529\) |
| \(5\) | \(1.02459\) | \[\begin{bmatrix} 1 \\ - 0.48800 \\ - 0.48800 \\\end{bmatrix}\] | \(1.2441\) |
The exact value of the eigenvalue is \(\lambda = 1\)
and the corresponding eigenvector is
\[\lbrack X\rbrack = \begin{bmatrix} 1 \\ - 0.5 \\ - 0.5 \\ \end{bmatrix}\]
Multiple Choice Test
(1). The eigenvalues of
\[\begin{bmatrix} 5 & 6 & 17 \\ 0 & - 19 & 23 \\ 0 & 0 & 37 \\ \end{bmatrix}\]
are
(A) \(- 19,\ \ 5,\ \ 37\)
(B) \(19,\ \ - 5,\ \ - 37\)
(C) \(2,\ \ - 3,\ \ 7\)
(D) \(3,\ \ - 5,\ \ 37\)
(2). If \(\begin{bmatrix} - 4.5 \\ - 4 \\ 1 \\ \end{bmatrix}\)is an eigenvector of \(\begin{bmatrix} 8 & - 4 & 2 \\ 4 & 0 & 2 \\ 0 & - 2 & - 4 \\ \end{bmatrix}\), the eigenvalue corresponding to the eigenvector is
(A) \(1\)
(B) \(4\)
(C) \(-4.5\)
(D) \(6\)
(3). The eigenvalues of the following matrix
\[\begin{bmatrix} 3 & 2 & 9 \\ 7 & 5 & 13 \\ 6 & 17 & 19 \\ \end{bmatrix}\]
are given by solving the cubic equation
(A) \(\lambda^{3} - 27\lambda^{2} + 167\lambda - 285\)
(B) \(\lambda^{3} - 27\lambda^{2} - 122\lambda - 313\)
(C) \(\lambda^{3} + 27\lambda^{2} + 167\lambda + 285\)
(D) \(\lambda^{3} + 23.23\lambda^{2} - 158.3\lambda + 313\)
(4). The eigenvalues of a \(4 \times 4\) matrix \(\left\lbrack A \right\rbrack\) are given as \(2, - 3,13\), and \(7\). The \(\left| \det\left( A \right) \right|\) then is
(A) \(546\)
(B) \(19\)
(C) \(25\)
(D) cannot be determined
(5). If one of the eigenvalues of \(\left\lbrack A \right\rbrack_{n \times n}\) is zero, it implies
(A) The solution to \(\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack\) system of equations is unique
(B) The determinant of \(\left\lbrack A \right\rbrack\) is zero
(C) The solution to \(\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack 0 \right\rbrack\) system of equations is trivial
(D) The determinant of \(\left\lbrack A \right\rbrack\) is nonzero
(6).Given that matrix \(\left\lbrack A \right\rbrack = \begin{bmatrix} 8 & - 4 & 2 \\ 4 & 0 & 2 \\ 0 & - 2 & - 3 \\ \end{bmatrix}\)has an eigenvalue value of 4 with the corresponding Eigenvectors of \(\left\lbrack x \right\rbrack = \begin{bmatrix} - 4.5 \\ - 4 \\ 1 \\ \end{bmatrix}\), then \(\left\lbrack A \right\rbrack^{5}\left\lbrack X \right\rbrack\) is
(A) \(\begin{bmatrix} - 18 \\ -16 \\ 4 \\ \end{bmatrix}\)
(B) \(\begin{bmatrix} -4.5 \\ -4 \\ 1 \\ \end{bmatrix}\)
(C) \(\begin{bmatrix} -4608 \\ -4096 \\ 1024 \\ \end{bmatrix}\)
(D) \(\begin{bmatrix} -0.004395 \\ -0.003906 \\ 0.0009766 \\ \end{bmatrix}\)
For complete solution, go to
https://ma.mathforcollege.com/mcquizzes/04sle/quiz_04sle_eigenvaluesandeigenvectors_solution.pdf
Eigenvalues and Eigenvectors Exercise
(1). The eigenvalues \(\lambda\) of matrix \(\lbrack A\rbrack\) are found by solving the equation(s)?
\(\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack I\rbrack\)
\(\lbrack A\rbrack\ \lbrack X\rbrack - \lambda\lbrack I\rbrack = 0\)
\(\left| A = 0 \right|\)
\(\left| A - \lambda I \right| = 0\)
Answer: D
(2). Find the eigenvalues and eigenvectors of
\[\lbrack A\rbrack = \begin{bmatrix} 10 & 9 \\ 2 & 3 \\ \end{bmatrix}\]
using the determinant method
Answer: \((12,1)\), \(\begin{bmatrix} 0.9762 \\ 0.2169 \\ \end{bmatrix}\), \(\begin{bmatrix} 0.8381 \\ - 0.8381 \\ \end{bmatrix}\)
(3). Find the eigenvalues and eigenvectors of
\[\lbrack A\rbrack = \begin{bmatrix} 4 & 0 & 1 \\ - 2 & 0 & 1 \\ 2 & 0 & 1 \\ \end{bmatrix}\]
using the determinant method
Answer: \((0,4,5615,0.43845)\), \(\begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix}\),\(\begin{bmatrix} 0.87193 \\ - 0.27496 \\ 0.48963 \\ \end{bmatrix}\),\(\begin{bmatrix} - 0.27816 \\ 3.5284 \\ 0.99068 \\ \end{bmatrix}\)
(4). Find the eigenvalues of these matrices by inspection
\(\begin{bmatrix} 2 & 0 & 0 \\ 0 & -3 & 0 \\ 0 & 0 & 6 \\ \end{bmatrix}\)
\(\begin{bmatrix} 3 & 5 & 7 \\ 0 & -2 & 1 \\ 0 & 0 & 0 \\ \end{bmatrix}\)
\(\begin{bmatrix} 2 & 0 & 0 \\ 3 & 5 & 0 \\ 2 & 1 & 6 \\ \end{bmatrix}\)
Answer:
\(2, -3,6\)
\(3, -2,0\)
\(2,5,6\)
(5). Find the largest eigenvalue in magnitude and its corresponding vector by using the power method
\[\lbrack A\rbrack = \begin{bmatrix} 4 & 0 & 1 \\ -2 & 0 & 1 \\ 2 & 0 & 1 \\ \end{bmatrix}\]
Start with an initial guess of the eigenvector as
\[\begin{bmatrix} 1 \\ -0.5 \\ 0.5 \\ \end{bmatrix}\]
Answer: 4.5615, \(\begin{bmatrix} 1 \\ -0.31534 \\ 0.56154 \\ \end{bmatrix}\)after 4 iterations
(6). Prove if \(\lambda\) is an eigenvalue of \(\lbrack A\rbrack\), then \(\frac{1}{\lambda}\) is an eigenvalue of \(\lbrack A\rbrack^{- 1}\).
(7). Prove that square matrices \(\lbrack A\rbrack\) and \(\lbrack A\rbrack^{T}\) have the same eigenvalues.
(8). Show that \(\left| \det(A) \right|\) is the product of the absolute values of the eigenvalues of \(\lbrack A\rbrack\).