Chapter 03.01: Prerequisites to Numerical Methods for Solving Nonlinear Equations
Learning Objectives
After successful completion of this lesson, you should be able to:
1) find the solutions of quadratic equations,
2) derive the formula for the solution of quadratic equations,
3) solve simple physical problems involving quadratic equations.
What are quadratic equations, and how do we solve them?
A quadratic equation has the form
\[ax^{2} + bx + c = 0,\ \text{where } a \neq 0\]
The solution to the above quadratic equation is given by
\[x = \frac{- b \pm \sqrt{b^{2} - 4ac}}{2a}\]
So the equation has two roots, and depending on the value of the discriminant, \(b^{2} - 4ac\), the equation may have real, complex, or repeated roots.
\[\text{If } b^{2} - 4ac < 0,\ \text{the roots are complex.}\]
\[\text{If } b^{2} - 4ac > 0,\ \text{the roots are real.}\]
\[\text{If } b^{2} - 4ac = 0,\ \text{the roots are real and repeated.}\]
Example 1
Derive the solution to \(ax^{2} + bx + c = 0\).
Solution
\[ax^{2} + bx + c = 0\;\;\;\;\;\;\;\;\;\;\;\; (E1.1)\]
Dividing both sides by \(a\), \(\left( a \neq 0 \right)\), we get
\[x^{2} + \frac{b}{a}x + \frac{c}{a} = 0\]
Note if \(a = 0\), the solution to
\[ax^{2} + bx + c = 0\]
is
\[x = - \frac{c}{b}\]
Rewrite Equation (E1.1) for \(a\neq0\)
\[x^{2} + \frac{b}{a}x + \frac{c}{a} = 0\]
as
\[\left( x + \frac{b}{2a} \right)^{2} - \frac{b^{2}}{4a^{2}} + \frac{c}{a} = 0\]
\[\begin{split} \left( x + \frac{b}{2a} \right)^{2}\ &= \frac{b^{2}}{4a^{2}} - \frac{c}{a}\\ &= \frac{b^{2} - 4ac}{4a^{2}} \end{split}\]
\[\begin{split} x + \frac{b}{2a} &= \pm \sqrt{\frac{b^{2} - 4ac}{4a^{2}}}\\ &= \pm \frac{\sqrt{b^{2} - 4ac}}{2a}\end{split}\]
\[\begin{split} x &= - \frac{b}{2a} \pm \frac{\sqrt{b^{2} - 4ac}}{2a}\\ &= \frac{- b \pm \sqrt{b^{2} - 4ac}}{2a} \end{split}\;\;\;\;\;\;\;\;\;\;\;\; (E1.2)\]
Example 2
A ball is thrown down at 50 mph from the top of a building. The building is 420 feet tall. Derive the equation that would let you find the time the ball takes to reach the ground.
Solution
The distance \(s\) covered by the ball is given by
\[s = ut + \frac{1}{2}gt^{2}\;\;\;\;\;\;\;\;\;\;\;\; (E2.1)\]
where
\[u = \text{initial velocity (ft/s)}\]
\[g = \text{acceleration due to gravity (ft}/\text{s}^2)\]
\[t = \text{time (s)}\]
Given
\[\begin{split} u &= {50}\frac{\text{miles}}{\text{hour}} \times \frac{1\text{ hour}}{3600\text{ s}} \times \frac{5280\text{ ft}}{1\text{ mile}}\\ &= { 73.33\ }\frac{\text{ft}}{\text{s}}\end{split}\]
\[g = \text{32.2}\frac{\text{ft}}{\text{s}^{2}}\]
\[s = 420\ \text{ft}\]
we have from Equation (2.1)
\[420 = 73.33t + \frac{1}{2}\left( 32.2 \right)\ t^{2}\]
\[16.1t^{2} + 73.33t - 420 = 0\]
The above equation is a quadratic equation, the solution of which would give the time it would take the ball to reach the ground. The solution of the quadratic equation is
\[\begin{split} t\ &= \frac{- 73.33 \pm \sqrt{73.33^{2} - 4 \times 16.1 \times ( - 420)}}{2(16.1)} \\ &= 3.315, - 7.870\end{split}\]
Since \(t > 0,\) the valid value of time \(t\) is \(3.315\ \text{s.}\)
Multiple Choice Test
(1). The value of \(x\) that satisfies \(f\left( x \right) = 0\) is called most suitably the
(A) root of an equation \(f\left( x \right) = 0\)
(B) root of a function \(f\left( x \right)\)
(C) zero of an equation \(f\left( x \right) = 0\)
(D) none of the above
(2). A quadratic equation has _______ root(s).
(A) one
(B) two
(C) three
(D) four
(3). For a certain cubic equation, at least one of the roots is known to be a complex root. How many complex roots does the cubic equation have?
(A) one
(B) two
(C) three
(D) cannot be determined
(4). An equation such as \(\tan x = x\) has _______ root(s).
(A) zero
(B) one
(C) two
(D) infinite
(5). A polynomial of order n has __________ zeros.
(A) \(n - 1\)
(B) \(n\)
(C) \(n + 1\)
(D) \(n + 2\)
(6). The velocity of a body is given by \(v(t) = 5e^{- t} + 4\), where t is in seconds and \(v\) is in m/s. The velocity of the body is \(6\) m/s at t = ____________ seconds.
(A) \(0.1823\)
(B) \(0.3979\)
(C) \(0.9163\)
(D) \(1.609\)
For complete solution, go to
http://nm.mathforcollege.com/mcquizzes/03nle/quiz_03nle_background_solution.pdf
Problem Set
(1). Find the roots of the equation \(2x^{2} + 5x =-3\).
Answer: \(-1.5,\ -1\)
(2). Find the roots of the equation \(2x^{2} + 4x + 4 = 0\).
Answer: \(-1+i,\ -1-i\)
(3). Using any method, estimate the smallest non-negative root of the equation \(\tan(x) = x\). Plot the function, \(\tan(x)\) and \(x\) to help you to find an approximate answer.
Answer: \(x=0\)
(4). You are working for ‘DOWN THE TOILET COMPANY’ that makes floats for ABC commodes. The ball has a specific gravity of \(0.6\) and has a radius of \(5.5\) cm. You are asked to find the depth to which the ball will get submerged when floating in water.
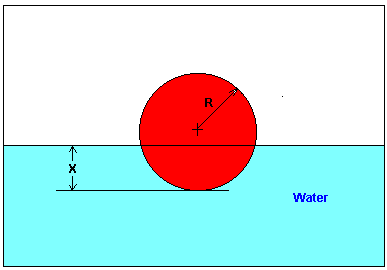
The equation that gives the depth \(x\) (unit of \(x\) is m) to which the ball is submerged under water is given by
\[x^{3} - 0.165x^{2} + 3.993 \times 10^{- 4} = 0\]
Note that the cubic equation will have three roots. Can some of these roots be complex. If so how many complex roots can it have? If more than one root of the above equation is real, how do you choose the acceptable root? Or are all the real roots physically acceptable?
Answer: The roots are \(0.062378,\ 0.14636,\ -0.043737\). Only \(x=0.062378\) is acceptable as the root needs to lie between \(0\) and the diameter, \(D=0.11m\).
(5). A ball is thrown down at \(50\) mph from the top of a building. The building is \(420\) feet tall. The time in seconds the ball would take to reach the ground is given by
\[{16.1}t^{2} + {73.33}t - {420} = 0{,\ t} \geq 0 \]
a) How many roots does the quadratic equation have?
b) Which of the two roots is a valid answer?
c) How much time would the ball take to reach the ground if it was just let go rather than thrown?
d) If the quadratic equation gave you complex roots, what would be your conclusion?
Answer: \(a)\ 2\ \ b)\ 3.3149\ s\ \ c)\ 5.1075\ s\ \ d)\ \text{Modeling of eqn must be wrong.}\)
(6). A straight steel ruler that is \(12^{\prime\prime}\) long at the initial temperature of \(80^{\circ}\)F contracts in length when dipped in a cold liquid. It is allowed to reach steady state. If the reduction in the length at steady state is found to be \(0.001^{\prime\prime}\), find the nonlinear equation (you do not have to solve it) that will allow you to find the temperature of the liquid. The reduction in the length, \(\Delta L\) is given by
\[\Delta L = L\int_{T_{\text{initial}}}^{T_{\text{liquid}}}{\alpha dT}\]
where
\[L = \text{initial length of the ruler,}\]
\[\alpha = - 1.2 \times 10^{- 11}T^{2} + 6.2 \times 10^{- 9}T + 6 \times 10^{- 6}\]
\[(\text{units of}\ \alpha\ \text{are}\ in/in/^{\circ}F,\ \text{and units of temperature are}\ ^{\circ}F)\]
\[T_{\text{liquid}}= \text{temperature of the liquid,}\]
\[T_{\text{initial}} = \text{initial temperature of the steel ruler.}\]
Answer: \(-4.8 \times 10^{-11} (T_{liquid})^{3}+3.72\times10^{-8}(T_{liquid})^{2}+7.2\times10^{-5}(T_{liquid})-4.9735\times10^{-3}=0\)