Chapter 02.02: Numerical Differentiation of Continuous Functions
Learning Objectives
After successful completion of this lesson, you should be able to:
1) derive formulas for approximating the first derivative of a function,
2) use the developed formulas in examples to estimate derivatives of a function.
Introduction
The first derivative of a function \(f\left( x \right)\) at \(x\) is defined as
\[f^{\prime}\left( x \right) = \lim_{h \rightarrow 0}\frac{f\left( x + h \right) - f\left( x \right)}{h}\]
To be able to find a derivative numerically, one could make \(h\) finite to give,
\[f^{\prime}\left( x \right) \approx \frac{f\left( x + h \right) - f\left( x \right)}{h}.\]
Knowing the value of \(x\) at which you want to find the derivative of \(f\left( x \right)\), we choose a finite value of \(h\) to find the value of \(f^{\prime}\left( x \right)\). To estimate the value of \(f^{\prime}\left( x \right)\), one such approximation is suggested as follows.
Forward Difference Approximation of the First Derivative
For a finite h,
\[f^{\prime}\left( x \right) \approx \frac{f\left( x + h \right) - f\left( x \right)}{h}\;\;\;\;\;\;\;\;\;\;\;\; (1)\]
The above is the forward divided difference approximation of the first derivative. It is called forward because you are taking a point ahead of \(x\).
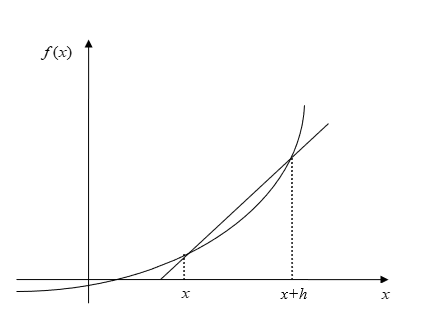
Figure 1: Graphical representation of forward difference approximation of first derivative.
Example 1
The velocity of a rocket is given by
\[v\left( t \right) = 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100t} \right\rbrack - 9.8t,\ 0 \leq t \leq 30\]
where \(v\) is given in m/s and \(t\) is given in seconds. At \(t = 16\ \text{s}\),
a) use the forward difference approximation of the first derivative of \(v\left( t \right)\) to calculate the acceleration. Use a step size of \(h = 2\ \text{s}\).
b) find the exact value of the acceleration of the rocket.
c) calculate the absolute relative true error for part (b).
Solution
(a) \[a\left( t \right) \approx \frac{v\left( t + h \right) - v\left( t \right)}{h}\]
\[t = 16\]
\[h = 2\]
\[\displaystyle a\left( 16 \right) \approx \frac{v\left( 18 \right) - v\left( 16 \right)}{2}\]
\[\begin{split} v\left( 18 \right) &= 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100\left( 18 \right)} \right\rbrack - 9.8\left( 18 \right)\\ &= 453.02\text{ m/s}\end{split}\]
\[\begin{split} v\left( 16 \right) &= 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100\left( 16 \right)} \right\rbrack - 9.8\left( 16 \right)\\ &= 392.07\text{ m/s}\end{split}\]
Hence
\[\begin{split} a\left( 16 \right) &\approx \frac{v\left( 18 \right) - v\left( 16 \right)}{2}\\ &= \frac{453.02 - 392.07}{2}\\ &= 30.474\ \text{m/s}^{2}\end{split}\]
(b) The exact value of \(a\left( 16 \right)\) can be calculated by differentiating
\[v\left( t \right) = 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100t} \right\rbrack - 9.8t\]
as
\[a\left( t \right) = \frac{d}{{dt}}\left\lbrack v\left( t \right) \right\rbrack\]
Knowing that
\[\frac{d}{{dt}}\left\lbrack \ln\left( {at} \right) \right\rbrack = \frac{1}{t},\ \text{and}\]
\[\frac{d}{{dt}}\left\lbrack \frac{a}{b - ct} \right\rbrack = - \frac{{ac}}{{(b - ct)}^{2}}\]
\[\begin{split} a\left( t \right) &= 2000\left( \frac{14 \times 10^{4} - 2100t}{14 \times 10^{4}} \right)\frac{d}{{dt}}\left( \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100t} \right) - 9.8\\ &= 2000\left( \frac{14 \times 10^{4} - 2100t}{14 \times 10^{4}} \right)\left( - 1 \right)\left( \frac{(14 \times 10^{4})\left( - 2100 \right)}{\left( 14 \times 10^{4} - 2100t \right)^{2}} \right) - 9.8\\ &= \frac{- 4040 - 29.4t}{- 200 + 3t}\end{split}\]
\[\begin{split} a\left( 16 \right) &= \frac{- 4040 - 29.4\left( 16 \right)}{- 200 + 3\left( 16 \right)}\\ &= 29.674\text{ m/s}^{2}\end{split}\]
(c) The absolute relative true error is
\[\begin{split} \left| \epsilon_{t} \right| &= \left| \frac{\text{True Value} - \text{Approximate Value}}{\text{True Value}} \right| \times 100\\ &= \left| \frac{29.674 - 30.474}{29.674} \right| \times 100\\ &= 2.6967\% \end{split}\]
Backward Difference Approximation of the First Derivative
We know
\[f^{\prime}\left( x \right) = \lim_{h \rightarrow 0}\frac{f\left( x + h \right) - f\left( x \right)}{h}\]
For a finite \(h\),
\[f^{\prime}\left( x \right) \approx \frac{f\left( x + h \right) - f\left( x \right)}{h}\]
If \(h\) is chosen as a negative number,
\[\begin{split} f^{\prime}\left( x \right) &\approx \frac{f\left( x - h \right) - f\left( x \right)}{- h}\\ &= \frac{f\left( x \right) - f\left( x - h \right)}{h}\;\;\;\;\;\;\;\;\;\;\;\; (2) \end{split}\]
This is a backward difference approximation as you are taking a point backward from \(x\).
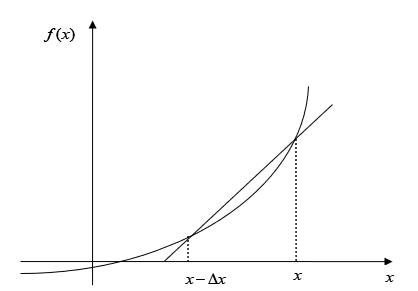
Figure 2: Graphical representation of backward difference approximation of the first derivative.
Example 2
The velocity of a rocket is given by
\[v\left( t \right) = 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100t} \right\rbrack - 9.8t,\ 0 \leq t \leq 30\]
(a) Use the backward difference approximation of the first derivative of \(v\left( t \right)\) to calculate the acceleration at \(t = 16\ \text{s}\). Use a step size of \(h = 2\ \text{s}\).
(b) Find the absolute relative true error for part (a).
Solution
(a) \[a\left( t \right) \approx \frac{v\left( t + h \right) - v\left( t \right)}{h}\]
\[t = 16\]
\[h = 2\]
\[a\left( 16 \right) \approx \frac{v\left( 16 \right) - v\left( 14 \right)}{2}\]
\[\begin{split} v\left( 16 \right) &= 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100\left( 16 \right)} \right\rbrack - 9.8\left( 16 \right)\\ &= 392.07\ \text{m/s} \end{split}\]
\[\begin{split} v\left( 14 \right) &= 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100\left( 14 \right)} \right\rbrack - 9.8\left( 14 \right)\\ &= 334.24\ \text{m/s} \end{split}\]
\[\begin{split} a\left( 16 \right) &\approx \frac{v\left( 16 \right) - v\left( 14 \right)}{2}\\ &= \frac{392.07 - 334.24}{2}\\ &= 28.915\ \text{m/s}^{2}\end{split}\]
(b) The exact value of the acceleration at \(t = 16\ \text{s}\) from Example 1 is
\[a\left( 16 \right) = 29.674\ \text{m/s}^{2}\]
The absolute relative true error for the answer in part (a) is
\[\begin{split} \left| \epsilon_{t} \right| &= \left| \frac{29.674 - 28.915}{29.674} \right| \times 100\\ &= 2.5584\% \end{split}\]
Central Divided Difference Approximation of the First Derivative
If we took a point forward and backward of \(x\) by a distance of \(h\), then the slope of the secant line (Rise/Run) as shown in Figure 3, and approximating it as the first derivative of the function at \(h,\)
\[\begin{split} f^{\prime}\left( x \right) &\approx \frac{f\left( x + h \right) - f\left( x - h \right)}{\left( x + h \right) - (x - h)}\\ &= \frac{f\left( x + h \right) - f\left( x - h \right)}{2h}\;\;\;\;\;\;\;\;\;\;\;\; (3)\end{split}\]
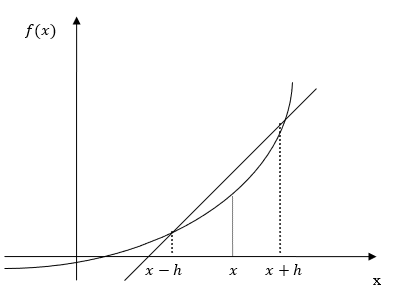
Figure 3. Graphical representation of central difference approximation of first derivative.
Example 3
The velocity of a rocket is given by
\[v\left( t \right) = 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100t} \right\rbrack - 9.8t,0 \leq t \leq 30.\]
(a) Use the central difference approximation of the first derivative of \(v\left( t \right)\) to calculate the acceleration at \(t = 16\ \text{s}\). Use a step size of \(h = 2\ \text{s}\).
(b) Find the absolute relative true error for part (a).
Solution
(a) \[a(t)\approx \frac{v(t+h) -v( t-h)}{2h}\]
\[t = 16\]
\[h = 2\]
\[\begin{split} a\left( 16 \right) &\approx \frac{v\left( 16 + 2 \right) - v\left( 16 - 2 \right)}{2\left( 2 \right)}\\ &= \frac{v\left( 18 \right) - v\left( 14 \right)}{4}\end{split}\]
\[\begin{split} v\left( 18 \right) &= 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100\left( 18 \right)} \right\rbrack - 9.8\left( 18 \right)\\ &= 453.02\ \text{m/s}\end{split}\]
\[\begin{split} v\left( 14 \right) &= 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100\left( 14 \right)} \right\rbrack - 9.8\left( 14 \right)\\ &= 334.24\ \text{m/s}\end{split}\]
\[\begin{split} a\left( 16 \right) &\approx \frac{v\left( 18 \right) - v\left( 14 \right)}{4}\\ &= \frac{453.02 - 334.24}{4}\\ &= 29.694\ \text{m/s}^{2}\end{split}\]
(b) The exact value of the acceleration at \(t = 16\ \text{s}\) from Example 1 was found as
\[a\left( 16 \right) = 29.674\ \text{m/s}^{2}\]
The absolute relative true error for the answer in part (a) is
\[\begin{split} \left| \epsilon_{t} \right| &= \left| \frac{\text{True Value} - \text{Approximate Value}}{\text{True Value}} \right| \times 100\\ &= \left| \frac{29.674 - 29.694}{29.674} \right| \times 100\\ &= 0.069157\% \end{split}\]
Order of Accuracy of Divided Difference Schemes
When using the divided difference schemes, errors are introduced due to their approximate nature. However the order of the error is not the same.
The order of accuracy in the forward divided difference method is of \(O\left( h \right).\)
\[f^{\prime}\left( x \right) = \frac{f\left( x + h \right) - f\left( x \right)}{h} + O\left( h \right)\;\;\;\;\;\;\;\;\;\;\;\; (4)\]
The order of accuracy in the backward divided difference method is of \(O\left( h \right).\)
\[f^{\prime}\left( x \right) = \frac{f\left( x \right) - f\left( x-h \right)}{h} + O\left( h \right) \;\;\;\;\;\;\;\;\;\;\;\; (5)\]
The order of accuracy in the central divided difference method is of \(O\left( h^2 \right).\)
\[f^{\prime}(x) = \frac{f(x+h) - f( x-h)}{2h} + O\left( h^2 \right) \;\;\;\;\;\;\;\;\;\;\;\; (6)\]
The derivation and application of the order of the accuracy of the three divided difference schemes as given by Equations (4)-(6) is given in the next lesson in the textbook.
Learning Objectives
After successful completion of this lesson, you should be able to:
1) derive formulas for approximating for higher-order derivatives,
2) use the developed formulas in examples to find higher derivatives of a function
Introduction
We used trigonometry and calculus to find the approximation of the first derivatives in the previous lessons. To find higher-order derivatives by such means is cumbersome and hinders a general approach to developing the numerical methods of approximating derivatives of any order.
One can use the Taylor series to approximate a higher-order derivative. As an illustration, here we derive the central difference approximation of the second derivative of a function \(f\left( x \right)\) .
The Taylor series is given by
\[f\left( x + h \right) = f\left( x \right) + f^{\prime}\left( x \right)\ h + \frac{f^{\prime\prime}\left( x \right)}{2!}\left( h \right)^{2} + \frac{f^{\prime\prime\prime}\left( x \right)}{3!}\left( h \right)^{3} + \frac{f^{\prime\prime\prime\prime}(x)}{4!}{(h)}^{4} + \ldots\;\;\;\;\;\;\;\;\;\;\;\; (1)\]
We can rewrite the Taylor series by substituting \(- h\) for \(h\),
\[f\left( x - h \right) = f\left( x \right) + f^{\prime}\left( x \right)\ ( - h) + \frac{f^{\prime\prime}\left( x \right)}{2!}\left( - h \right)^{2} + \frac{f^{\prime\prime\prime}\left( x \right)}{3!}\left( - h \right)^{3} + \frac{f^{\prime\prime\prime\prime}(x)}{4!}{( - h)}^{4}+\ldots\]
to get
\[f\left( x - h \right) = f\left( x \right) - f^{\prime}\left( x \right)\ h + \frac{f^{\prime\prime}\left( x \right)}{2!}h^{2} - \frac{f^{\prime\prime\prime}\left( x \right)}{3!}h^{3} + \frac{f^{\prime\prime\prime\prime}(x)}{4!}h^{4}+\ldots\;\;\;\;\;\;\;\;\;\;\;\; (2)\]
Adding Equations (1) and (2) gives
\[f\left( x + h \right) + f\left( x - h \right) = 2f\left( x \right) + 2\frac{f^{\prime\prime}\left( x \right)}{2!}h^{2} + 2\frac{f^{\prime\prime\prime\prime}(x)}{4!}h^{4} + \ldots\]
Moving all terms other than the \(f^{\prime\prime}\left( x \right)\) to the left side
\[f\left( x + h \right) + f\left( x - h \right) - 2f\left( x \right) - 2\frac{f^{\prime\prime\prime\prime}(x)}{4!}h^{4} - \ldots = f^{\prime\prime}\left( x \right)h^{2}\]
\[f^{\prime\prime}\left( x \right) = \frac{f\left( x + h \right) - 2f\left( x \right) + f\left( x - h \right)}{h^{2}} - 2\frac{f^{\prime\prime\prime\prime}(x)}{4!}h^{2} - \ldots\]
Hence
\[f^{\prime\prime}\left( x \right) \approx \frac{f\left( x + h \right) - 2f\left( x \right) + f\left( x - h \right)}{h^{2}}\;\;\;\;\;\;\;\;\;\;\;\; (3)\]
Example 1
The velocity of a rocket is given by
\[v\left( t \right) = 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100t} \right\rbrack - 9.8t,\ 0 \leq t \leq 30,\]
(a) Use the central difference approximation of the second derivative of \(v\left( t \right)\) to calculate the jerk at \(t = 16\ \text{s}\). Use a step size of \(h = 2\ \text{s}\).
Solution
The second derivative of velocity with respect to time is called jerk. The second-order approximation of jerk then is
\[j\left( t \right) \approx \frac{v\left( t + h \right) - 2v\left( t \right) + v\left( t - h \right)}{h^{2}}\]
\[t = 16\]
\[h = 2\]
\[\begin{split} t + h &= 16 + 2\\ &= 18\end{split}\] \[\begin{split} t - h &= 16 - 2\\ &= 14\end{split}\]
\[j\left( 16 \right) \approx \frac{v\left( 18 \right) - 2v\left( 16 \right) + v\left( 14 \right)}{\left( 2 \right)^{2}}\]
\[\begin{split} v\left( 18 \right)&= 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100\left( 18 \right)} \right\rbrack - 9.8\left( 18 \right)\\ &= 453.02 \text{ m/s}\end{split}\]
\[\begin{split} v\left( 16 \right) &= 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100\left( 16 \right)} \right\rbrack - 9.8\left( 16 \right)\\ &= 392.07\ \text{m/s}\end{split}\]
\[\begin{split} v\left( 14 \right) &= 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100\left( 14 \right)} \right\rbrack - 9.8\left( 14 \right)\\ &= 334.24\ \text{m/s}\end{split}\]
Hence
\[\begin{split} j\left( 16 \right) &\approx \frac{v\left( 18 \right) - 2v\left( 16 \right) + v\left( 14 \right)}{\left( 2 \right)^{2}}\\ &= \frac{453.02 - 2\left( 392.07 \right) + 334.24}{4}\\ &= 0.77969\ \text{m/s}^{3}\end{split}\]
(b) The exact value of \(j\left( 16 \right)\) can be calculated by differentiating
\[v\left( t \right) = 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100t} \right\rbrack - 9.8t\]
twice.
Now
\[a\left( t \right) = \frac{d}{{dt}}\left\lbrack v\left( t \right) \right\rbrack\]
Knowing that
\[\frac{d}{{dt}}\left\lbrack \ln\left( {at} \right) \right\rbrack = \frac{1}{t},\ \text{and}\]
\[\frac{d}{{dt}}\left\lbrack \frac{a}{b - ct} \right\rbrack = - \frac{{ac}}{{(b - ct)}^{2}}\]
\[\begin{split} a\left( t \right) &= 2000\left( \frac{14 \times 10^{4} - 2100t}{14 \times 10^{4}} \right)\frac{d}{{dt}}\left( \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100t} \right) - 9.8\\ &= 2000\left( \frac{14 \times 10^{4} - 2100t}{14 \times 10^{4}} \right)\left( - 1 \right)\left( \frac{(14 \times 10^{4})\left( - 2100 \right)}{\left( 14 \times 10^{4} - 2100t \right)^{2}} \right) - 9.8\\ &= \frac{- 4040 - 29.4t}{- 200 + 3t}\end{split}\]
\[\begin{split} j\left( t \right) &= \frac{d}{{dt}}\left\lbrack a\left( t \right) \right\rbrack\\ &= \frac{d}{{dt}}\left\lbrack \frac{- 4040 - 29.4t}{- 200 + 3t} \right\rbrack \end{split}\]
Knowing that
\[\frac{d}{{dt}}\left\lbrack \frac{a + bt}{c + dt} \right\rbrack = - \frac{ad - bc}{{(c + dt)}^{2}}\]
we get
\[j\left( t \right) = \frac{18000}{{( - 200 + 3t)}^{2}}\]
Hence
\[\begin{split} j\left( 16 \right) &= - \frac{\left( - 4040)(3 \right) - \left( - 29.4 \right)( - 200)}{\left( - 200 + 3\left( 16 \right) \right)^{2}}\\ &= 0.77908\ \text{m/s}^{3}\end{split}\]
The absolute relative true error is
\[\begin{split} \left| \epsilon_{t} \right| &= \left| \frac{\text{True Value} - \text{Approximate Value}}{\text{True Value}} \right| \times 100\\ &= \left| \frac{0.77908 - 0.77969}{0.77908} \right| \times 100\\ &= 0.077992\% \end{split}\]
Learning Objectives
After successful completion of this lesson, you should be able to:
1) derive formulas from the Taylor series for approximating the first derivative of a function,
2) find the order of accuracy of divided difference formulas
3) use the order of accuracy results to derive more efficient numerical methods such as Richardson’s extrapolation formula.
Introduction
The finite difference formulas we develop in previous lessons for the first and second derivatives of a function are approximate, as they have a truncation error.
Look at the example from the previous lessons, which asked to find the value of the acceleration (first derivative) at \(t = 16{s}\) using a step size of \(h = 2{ s}\) by forward, backward, and central divided difference formulas. The velocity of a rocket was given by
\[v\left( t \right) = 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100t} \right\rbrack - 9.8t,0 \leq t \leq 30.\]
The results, along with the relative approximate true errors from the three difference approximations, are given in Table 1.
Table 1. Summary of \(a\left( {16} \right)\) using different difference approximations
\(\text{Type of difference}\) \(\text{approximation}\) |
\(a(16)\) \(({m/}{s^2})\) |
\(\left | \epsilon_{t} \right|\%\) |
|---|---|---|
\(\text{Forward}\) \(\text{Backward}\) \(\text{Central}\) |
\(30.475\) \(28.915\) \(29.695\) |
\(2.6967\) \(2.5584\) \(0.069157\) |
So the question arises that why is the central divided difference (CDD) approximation better than the forward divided difference (FDD) and backward divided difference (BDD) approximations. Is it an isolated case? The true errors in the forward and backward divided difference approximations are of the same order. Is that also an isolated case? To illustrate this, we derive the order of accuracy of the three divided difference schemes.
Example 1
The forward divided difference scheme for finding the approximate first derivative of a function \(f\left( x \right)\) is given by
\[f^{\prime}\left( x \right) \approx \frac{f\left( x + h \right) - f\left( x \right)}{h}\]
Show that the order of the accuracy of the above formula is of the order of \(h\).
Solution
Taylor’s theorem says that if you know the value of a function \(f(x)\) at a point \(x\) and all its derivatives at that point, provided the derivatives are continuous between \(x\) and \(x + h\), then
\[f\left( x + h \right) = f\left( x \right) + f^{\prime}\left( x \right)h + \frac{f^{\prime\prime}\left( x \right)}{2!}h^{2} + \frac{f^{\prime\prime\prime}\left( x \right)}{3!}h^{3} + \ldots\;\;\;\;\;\;\;\;\;\;\;\; (E1.1)\]
Taking the first term of the right-hand side of Equation (1) to the left-hand side
\[f\left( x + h \right) - f\left( x \right) = f^{\prime}\left( x \right)h + \frac{f^{\prime\prime}\left( x \right)}{2!}h^{2} + \frac{f^{\prime\prime\prime}\left( x \right)}{3!}h^{3} + \ldots\]
Taking the first derivative term to the left-hand side and the function terms to the right-hand side
\[f^{\prime}\left( x \right)h = f\left( x + h \right) - f\left( x \right) - \frac{f^{\prime\prime}\left( x \right)}{2!}h^{2} - \frac{f^{\prime\prime\prime}\left( x \right)}{3!}h^{3} - \ldots\]
Dividing both sides by \(h\), to find \(f^{\prime}\left( x \right)\) gives
\[f^{\prime}\left( x \right) = \frac{f\left( x + h \right) - f\left( x \right)}{h} - \frac{f^{\prime\prime}\left( x \right)}{2!}h - \frac{f^{\prime\prime\prime}\left( x \right)}{3!}h^{2} - \ldots\;\;\;\;\;\;\;\;\;\;\;\; (E1.2)\]
The truncation error in the FDD formula for \(f^\prime(x)\) is hence given by
\[E_{t} = - \frac{f^{\prime\prime}\left( x \right)}{2!}h - \frac{f^{\prime\prime\prime}\left( x \right)}{3!}h^{2} - \ldots\;\;\;\;\;\;\;\;\;\;\;\; (E1.3)\]
For small values of \(h\), the predominant terms will be the first one in Equation (6), and hence the order of accuracy is determined to be of the \(O\left( h \right).\)
\[f^{\prime}\left( x \right) = \frac{f\left( x + h \right) - f\left( x \right)}{h} + O\left( h \right)\;\;\;\;\;\;\;\;\;\;\;\; (E1.4)\]
If you repeat the process for BDD, you will find the same order of accuracy
\[f^{\prime}\left( x \right) = \frac{f\left( x \right) - f\left( x-h \right)}{h} + O\left( h \right) \text{ for BDD.} \;\;\;\;\;\;\;\;\;\;\;\; (E1.5)\]
Example 2
The central divided difference scheme for finding the approximate first derivative of a function \(f\left( x \right)\) is given by
\[f^{\prime}\left( x \right) \approx \frac{f\left( x + h \right) - f\left( x - h \right)}{2h}\]
Show that the order of the accuracy of the above formula is of the order of \(h^{2}\).
Solution
Using the Taylor series, we write the value of the function \(f\left( x \right)\) at \(\left( x + h \right)\) in terms of the value of the function and its derivatives at \({x }\)as
\[f\left( x + h \right) = f\left( x \right) + f^{\prime}\left( x \right)h + \frac{f^{\prime\prime}\left( x \right)}{2!}h^{2} + \frac{f^{\prime\prime\prime}\left( x \right)}{3!}h^{3} + \frac{f^{\prime\prime\prime\prime}\left( x \right)}{4!}h^{4} + \frac{f^{\prime\prime\prime\prime\prime}\left( x \right)}{5!}h^{5} + \ldots\;\;\;\;\;\;\;\;\;\;\;\; (E2.1)\]
Using the Taylor series again, we write the value of the function \(f\left( x \right)\)at \(\left( x - h \right)\) in terms of the value of the function and its derivatives at \({x }\)as (simply done by substituting \(\left( - h \right)\) for \(h\) in Equation (1)
\[\begin{split} f\left( x - h \right) &= f\left( x \right) + f^{\prime}\left( x \right)( - h) + \frac{f^{\prime\prime}\left( x \right)}{2!}( - h)^{2} + \frac{f^{\prime\prime\prime}\left( x \right)}{3!}( - h)^{3} + \frac{f^{\prime\prime\prime\prime}\left( x \right)}{4!}\left( - h \right)^{4}\\ & \ \ \ + \frac{f^{\prime\prime\prime\prime\prime}\left( x \right)}{5!}{( - h)}^{5} + \ldots\\ &=f(x)-f^{\prime} (x)h+ \frac{{f^{\prime\prime}(x))}}{2!}h^2 - \frac{{f^{\prime\prime\prime}(x))}}{3!}h^3+\frac{{f^{\prime\prime\prime\prime}(x))}}{4!}h^4-\frac{{f^{\prime\prime\prime\prime\prime}(x))}}{5!}h^5+\ldots\;\;\;\;\;\;\;\;\;\;\;\; (E2.2) \end{split}\]
Subtracting Equation (E2.2) from Equation (E2.1) gives
\[f\left( x + h \right) - f\left( x - h \right) = 2f^{\prime}\left( x \right)h + \frac{2f^{\prime\prime\prime}\left( x \right)}{3!}h^{3} + \frac{2f^{\prime\prime\prime\prime\prime}\left( x \right)}{5!}h^{5} + \ldots\;\;\;\;\;\;\;\;\;\;\;\; (E2.3)\]
Taking the first derivative term to the left-hand side and the function terms to the right-hand side
\[2f^{\prime}\left( x \right)h = f\left( x + h \right) - f\left( x - h \right) - \frac{2f^{\prime\prime\prime}\left( x \right)}{3!}h^{3} - \frac{2f^{\prime\prime\prime\prime\prime}\left( x \right)}{5!}h^{5} + \ldots\;\;\;\;\;\;\;\;\;\;\;\; (E2.4)\]
Dividing both sides by \(2h\), to find \(f^{\prime}\left( x \right)\) gives
\[f^{\prime}\left( x \right) = \frac{f\left( x + h \right) - f\left( x - h \right)}{2h} - \frac{f^{\prime\prime\prime}\left( x \right)}{3!}h^{2} - \frac{f^{\prime\prime\prime\prime\prime}\left( x \right)}{5!}h^{4} - \ldots\;\;\;\;\;\;\;\;\;\;\;\; (E2.5)\]
The truncation error in the CDD formula for \(f^{\prime}\left( x \right)\) is hence given by
\[E_{t} = - \frac{f^{\prime\prime\prime}\left( x \right)}{3!}h^{2} - \frac{f^{\prime\prime\prime\prime\prime}\left( x\right)}{5!}h^{4} - \ldots\;\;\;\;\;\;\;\;\;\;\;\; (E2.6)\]
For small values of \(h\), the predominant terms will be the first one in Equation (E2.6), and hence the order of accuracy is determined to be of the \(O\left( h^{2} \right).\)
\[f^{\prime}\left( x \right) = \frac{f\left( x + h \right) - f\left( x - h \right)}{2h} + O\left( h^{2} \right)\;\;\;\;\;\;\;\;\;\;\;\; (E2.7)\]
Since the order of accuracy is higher for CDD than FDD and BDD, the true error being much smaller in CDD is not an isolated incident. Since the order of accuracy is of similar order in FDD and BDD, the true error being of a similar order for FDD and BDD is not an isolated incident either.
Example 3
To further investigate the issue of the true error for CDD being of the order of the square of the step size, that is, \(h^2\), take the example of being asked to find the approximate value of the first derivative of \(2e^{1.5x}\)at \(x = 3\) using CDD scheme. The exact value (up to 5 significant digits) using differential calculus is found to be \(=270.05\). The central divided difference approximation of the first derivative with \(h = 0.1\) and then continuing to halve the step size are given in Table 2.
Table 2. Effect of step size on the error in CDD
\(\text{Step Size,}\) \(h\) |
\(\text{Central Divided Difference Approximation}\) \(\frac{f(x+h) - f(x-h)}{2h}\) |
\(\text{True Error} =\ \text{True Value}\ -\) \(\text{Approximate Value}\) |
|---|---|---|
| \(0.1\) | \(271.07\) | \(-1.0138\) |
| \(0.05\) | \(270.30\) | \(-0.25324\) |
| \(0.025\) | \(270.11\) | \(-0.06330\) |
| \(0.0125\) | \(270.06\) | \(-0.015824\) |
| \(0.00625\) | \(270.05\) | \(-0.0039558\) |
Comment on your observation of how the true error reduces with the step size.
Solution
In Table 2, we can observe that as the step size is halved, the true error is getting approximately quartered. This observation is in line with the derivation of the true error being of the order of \(h^{2}\). Let’s look at the contribution of the truncation terms as the step size decreases. That information is given in Table 3. The second column shows the true error.
Table 3. Contribution to true error as step size decreases in CDD.
\(\text{step size,}\) \(h\) |
\(\text{True Error}\) \(E_t\) |
\(\text{First Term of True Error}\) \(-\displaystyle\frac{f^{\prime\prime\prime}(x_i)}{3!}h^2\) |
\(\text{Rest of the True Error}\) \(-\displaystyle\frac{f^{\prime\prime\prime\prime\prime}(x_i)}{5!}h^4-...\) |
\(\text{True Error divided by}\) \(h^2\) |
|---|---|---|---|---|
| \(0.1\) | \(-1.0138\) | \(-1.0127\) | \(- 1. 1399 \times 10^{- 3}\) | \(-101.38\) |
| \(0.05\) | \(-0.25324\) | \(-0.25317\) | \(- 7. 1216 \times 10^{- 5}\) | \(-101.30\) |
| \(0.025\) | \(-0.06330\) | \(-0.063293\) | \(- 4. 4520 \times 10^{- 6}\) | \(-101.27\) |
| \(0.0125\) | \(-0.015824\) | \(-0.015823\) | \(- 2. 7970 \times 10^{- 7}\) | \(-101.27\) |
| \(0.00625\) | \(-0.0039558\) | \(-0.0039556\) | \(- 1. 8955 \times 10^{- 8}\) | \(-101.27\) |
In Table 3, you are able to see that the magnitude of the first term of the true error is much bigger than the magnitude of the rest of the true error terms and hence dominates the magnitude of the true error. Note that the value of the true error divided by \(h^{2}\) also gets close to be a constant as \({h }\)becomes smaller. In fact, the value would converge to the coefficient term of \(h^{2}\) in the true error term in Equation (6) which is \(110.27\) and is calculated as follows.
\[f\left( x \right) = 2e^{1.5x}\]
\[\begin{split} f^{\prime}(x) &= 2(1.5)e^{1.5x}\\ &= 3e^{1.5x} \end{split}\]
\[\begin{split} f^{\prime\prime}\left( x \right) &= 3(1.5)e^{1.5x}\\ &= 4.5e^{1.5x} \end{split}\]
\[\begin{split} f^{\prime\prime\prime}\left( x \right) &= 4.5(1.5)e^{1.5x}\\ &= 6.750e^{1.5x} \end{split}\]
Hence,
\[\begin{split} \frac{f^{\prime\prime\prime}(x)}{3!}\ &= \frac{6.750e^{1.5x}}{3!}\\ &= 110.27 \end{split}\]
This value of \(110.27\) is close to the number we have in the last column of Table 3 as \(h\) becomes small.
Richardson’s Extrapolation Formula for Central Divided Difference Approximation of First Derivative
Recognizing that the true error in the central divided difference formula for the first derivative is of the order the square of the step size, it allows us to develop more computationally efficient formulas for differentiation. These formulas are called Richardson’s extrapolation formulas for numerical differentiation.
Since the true error
\[E_{t} = O(h^{2})\]
\[E_{t} \approx Ch^{2}\;\;\;\;\;\;\;\;\;\;\;\; (1)\]
Let \({(AV)}_{h}\) denote the approximate value of the first derivative as calculated by using the equation
\[f^{\prime}\left( x \right) \approx \frac{f\left( x + h \right) - f\left( x - h \right)}{2h}\;\;\;\;\;\;\;\;\;\;\;\; (2)\]
and using the definition
\[E_{t} = \text {True Value - Approximate Value}\;\;\;\;\;\;\;\;\;\;\;\; (3)\]
we get,
\[Ch^{2} \approx \left( {TV} \right) - {({AV})}_{h}\;\;\;\;\;\;\;\;\;\;\;\; (4)\]
where,
\[{TV} = \text{True value}\]
If we decrease the step size by half to \(\displaystyle \frac{h}{2}\) , and \(\displaystyle {(AV)}_{\frac{h}{2}}\) denotes the approximate value of the first derivative calculated using the central divided difference equation, then
\[\displaystyle C\left( \frac{h}{2} \right)^{2} \approx \left( {TV} \right) - {({AV})}_{\frac{h}{2}}\;\;\;\;\;\;\;\;\;\;\;\; (5)\]
Multiplying Equation (5) by 4, gives
\[Ch^{2} \approx 4\left( {TV} \right) - 4{({AV})}_{\frac{h}{2}}\;\;\;\;\;\;\;\;\;\;\;\; (6)\]
Subtracting Equation (6) from Equation (4) gives
\[Ch^{2} - Ch^{2} \approx \left( \left( {TV} \right) - \left( {AV} \right)_{h} \right) - \left( 4\left( {TV} \right) - 4{({AV})}_{\frac{h}{2}} \right)\]
\[0 \approx - 3\left( {TV} \right) - \left( {AV} \right)_{h} + 4{({AV})}_{\frac{h}{2}}\]
Taking the \(\left( {TV} \right)\) term to the left side,
\[\displaystyle \begin{split} 3\left( {TV} \right) &\approx - \left( {AV} \right)_{h} + 4{({AV})}_{\frac{h}{2}}\\ \left( {TV} \right) &\approx \frac{- \left( {AV} \right)_{h} + 4{({AV})}_{\frac{h}{2}}}{3} \end{split}\;\;\;\;\;\;\;\;\;\;\;\; (7)\]
The above formula will allow us to find a better estimate of the first derivative just from the approximate values obtained using the step sizes \(h\) and \(\displaystyle \frac{h}{2}\) .
Equation (7) is generally rewritten as
\[\begin{split} \left( {TV} \right) &\approx \frac{- \left( {AV} \right)_{h} + 3\left( {AV} \right)_{\frac{h}{2}} + \left( {AV} \right)_{\frac{h}{2}}}{3}\\ &=(AV)_{\frac{h}{2}} + \frac{(AV)_{\frac{h}{2}}-(AV)_{h}}{3}\end{split}\;\;\;\;\;\;\;\;\;\;\;\; (8)\]
One of the reasons to write it this way is to show that adding a third of the difference between the approximate values obtained using step sizes of \(h\) and \(\displaystyle \frac{h}{2}\) to the most recent approximate value will give you a better estimate of the true value.
Example 4
Table 4 shows the approximate values of the first derivative of \(f\left( x \right) = 2e^{1.5x}\) at \(x = 3\) using different step sizes for the central divided difference scheme. Use the last two values of the scheme and Richardson’s extrapolation formula to get a better estimate of \(f^{\prime}(3)\).
Table 4. CDD approximate values as a function of step size
\(\text{Step Size,}\) \(h\) |
\(\text{Central Divided Difference}\) \(\text{Approximation}\) |
|---|---|
| \(0.1\) | \(271.07\) |
| \(0.05\) | \(270.30\) |
| \(0.025\) | \(270.11\) |
Solution
Using the last two values, we have
\[{({AV})}_{0.05} \approx 270.30\]
\[{({AV})}_{0.025} \approx 270.11\]
Using Equation (8)
\[\begin{split} TV &\approx {\ ({AV})}_{\frac{h}{2}} + \frac{\left( {AV} \right)_{\frac{h}{2}} - \left( {AV} \right)_{h}}{3}\\ &= (AV)_{0.025} + \frac{\left( {AV} \right)_{0.025} - \left( {AV} \right)_{0.05}}{3}\\ &= 270.11 + \frac{270.11 - 270.30}{3}\\ &= 270.05 \end{split}\]
Coincidentally, this is the exact value of \(f^\prime(3)\) up to 5 significant digits.
Example 5
Using
\[f^{\prime}\left( x \right) \approx \frac{f\left( x + h \right) - f\left( x - h \right)}{2h}\;\;\;\;\;\;\;\;\;\;\;\; (16)\]
two approximate values of \(f^{\prime}\left( 10 \right)\) are calculated using two different values of the step size \(h\).
For \(h = 2\), \[f^{\prime}\left( 10 \right) \cong 1315.\]
For \(h = 0.5\), \[f^{\prime}\left( 10 \right) \cong 626.\]
Based on this information, can you get a better estimate of \(f^{\prime}\left( 10 \right)\)? Find it.
Solution
The above approximate formula
\[f^{\prime}\left( x \right) \approx \frac{f\left( x + h \right) - f\left( x - h \right)}{2h}\]
is the central divided difference formula for \(f^{\prime}\left( x \right)\).
The true error, \(E_{t\ }\)associated with the formula is of the order of \(h^{2}\). Hence the true error for a step size of \(h_1\) is approximately \(C{h_{1}}^{2}\), where \(C\) is a constant of proportionality.
Since
\[\text{True Error} = \text{True Value} - \text{Approximate Value}\]
we have
\[C{h_{1}}^{2} \approx {TV} - ({AV})_{h_{1}}\;\;\;\;\;\;\;\;\;\;\;\; (E5.1)\]
where
\[TV = \text{True value} \text{ of } f^{\prime}\left( x \right)\]
\[(AV)_{h_{1}} = \text{ Approximate Value of } f^{\prime}\left( x \right) \text{ using step size } h_{1}\]
Similarly, for a different step size \(h_{2}\), the true error for a step size of \(h_{2}\) is approximately \(C{h_{2}}^{2}\).
Since
\[\text{True Error} = \text{True Value} - \text{Approximate Value}\]
\[C{h_{2}}^{2} \approx {TV} - ({AV})_{h_{2}}\;\;\;\;\;\;\;\;\;\;\;\; (E5.2)\]
where
\[(AV)_{h_{2}}= \text{ Approximate Value of } f^{\prime}\left( x \right) \text{ using step size } h_{2}\]
Dividing Equation (E5.1) by Equation (E5.2), we get
\[\frac{C{h_{1}}^{2}}{C{h_{2}}^{2}} \approx \frac{{TV} - ({AV})_{h_{1}}}{{TV} - ({AV})_{h_{2}}}\]
which gives
\[{TV} \approx \frac{({AV})_{h_{1}}{h_{2}}^{2} - ({AV})_{h_{2}}{h_{1}}^{2}}{\left( h_{2} - h_{1} \right)\left( h_{2} + h_{1} \right)}\;\;\;\;\;\;\;\;\;\;\;\; (E5.3)\]
In our case,
\[{h_{1} = 2,\ ({AV})_{h_{1}} = 1315,}\]
\[{h_{2} = 0.5,\ ({AV})_{h_{2}} = 626,}\]
Then from Equation (E5.3), we get
\[\begin{split} TV &\approx \frac{({AV})_{h_{1}}{h_{2}}^{2} - ({AV})_{h_{2}}{h_{1}}^{2}}{\left( h_{2} - h_{1} \right)\left( h_{2} + h_{1} \right)}\\ &= \frac{1315 \times 0.5^{2} - 626 \times 2^{2}}{\left( 0.5 - 2 \right)\left( 0.5 + 2 \right)}\\ &= 580.1 \end{split}\]
Appendix
The formulas for the first derivative of a continuous function talked about in this and the previous lessons for forward and backward divided difference have the accuracy of the order of the step-size.
For FDD
\[f^{\prime}\left( x \right) = \frac{f\left( x + h \right) - f\left( x \right)}{h} + O\left( h \right)\;\;\;\;\;\;\;\;\;\;\;\; (A.1)\]
For BDD
\[f^{\prime}\left( x \right) = \frac{f\left( x \right) - f\left( x - h \right)}{h} + O\left( h \right)\;\;\;\;\;\;\;\;\;\;\;\; (A.2)\]
The question arises, are there more accurate formulas for the forward and backward divided difference for the first derivative of a function. Yes, there are and they are also derivable by manipulating the Taylor series. For example, note the following.
For FDD, we can derive the three-point formula
\[f^{\prime}\left( x \right) = \frac{- 3f\left( x \right) + 4f\left( x + h \right) - f\left( x + 2h \right)}{2h} + O\left( h^{2} \right)\;\;\;\;\;\;\;\;\;\;\;\; (A.3)\]
For BDD, we can derive the three-point formula
\[f^{\prime}\left( x \right) = \frac{f\left( x - 2h \right) - 4f\left( x - h \right) + 3f(x)}{2h} + O\left( h^{2} \right)\;\;\;\;\;\;\;\;\;\;\;\; (A.4)\]
Both the above formulas have the same accuracy as the two-point CDD formula
\[f^{\prime}\left( x \right) = \frac{f\left( x + h \right) - f\left( x - h \right)}{2h} + O\left( h^{2} \right)\;\;\;\;\;\;\;\;\;\;\;\; (A.5)\]
Getting matching accuracy becomes critical in the efficiency of solving for an application where one may be forced to use combinations of the FDD, BDD, and CDD formulas.
Multiple Choice Test
(1). The definition of the first derivative of a function \(f(x)\) is
(A) \(\displaystyle f^{\prime}(x) = \frac{f(x + \Delta x) + f(x)}{{\Delta x}}\)
(B) \(\displaystyle f^{\prime}(x) = \frac{f(x + \Delta x) - f(x)}{{\Delta x}}\)
(C) \(\displaystyle f^{\prime}(x) = \lim_{{\Delta x} \rightarrow 0}\frac{f(x + \Delta x) + f(x)}{{\Delta x}}\)
(D) \(\displaystyle f^{\prime}(x) = \lim_{{\Delta x} \rightarrow 0}\frac{f(x + \Delta x) - f(x)}{{\Delta x}}\)
(2). The exact derivative of \(f(x) = x^{3}\) at \(x = 5\) is most nearly
(A) \(25.00\)
(B) \(75.00\)
(C) \(106.25\)
(D) \(125.00\)
(3). Using the forwarded divided difference approximation with a step size of \(0.2\), the derivative of \(f(x) = 5e^{2.3x}\) at \(x = 1.25\) is
(A) \(163.4\)
(B) \(203.8\)
(C) \(211.1\)
(D) \(258.8\)
(4). A student finds the numerical value of \(\displaystyle \frac{d}{{dx}}(e^{x}) = 20.220\) at \(x = 3\) using a step size of \(0.2\). Which of the following methods did the student use to conduct the differentiation?
(A) Backward divided difference
(B) Calculus, that is, exact
(C) Central divided difference
(D) Forward divided difference
(5). Using the backward divided difference approximation, \(\displaystyle \frac{d}{{dx}}(e^{x}) = 4.3715\) at \(x = 1.5\) for a step size of \(0.05\). If you keep halving the step size to find \(\displaystyle \frac{d}{{dx}}(e^{x})\) at \(x = 1.5\) before two significant digits can be considered to be at least correct in your answer, the step size would be (you cannot use the exact value to determine the answer)
(A) \(0.05/2\)
(B) \(0.05/4\)
(C) \(0.05/8\)
(D) \(0.05/16\)
(6). The heat transfer rate \(q\) over a surface is given by
\[\displaystyle q = - {kA}\frac{{dT}}{{dy}}\]
where
\[k = \text{thermal conductivity}\ \left( \frac{\text{J}}{\text{s} \cdot \text{m} \cdot \text{K}} \right)\]
\[A = \text{surface area}\ \left( \text{m}^{2} \right)\]
\[T = \text{temperature}\ (\text{K})\]
\[y = \text{distance normal to the surface}\ \left( \text{m} \right)\]
Given
\[k = 0.025\frac{\text{J}}{\text{s} \cdot \text{m} \cdot \text{K}}\]
\[A = 3{\ }\text{m}^{2}\]
the temperature \(T\) over the surface varies as
\[T = - 1493y^{3} + 2200y^{2} - 1076y + 500\]
The heat transfer rate \(q\) at the surface most nearly is
(A) \(-1076\ \text{W}\)
(B) \(37.5\ \text{W}\)
(C) \(80.7\ \text{W}\)
(D) \(500\ \text{W}\)
For complete solution, go to
http://nm.mathforcollege.com/mcquizzes/02dif/quiz_02dif_continuous_solution.pdf
Problem Set
(1). Find the exact value of \(\displaystyle \frac{{dy}}{{dx}}(x = 5)\), given
\[y = e^{x} + \sin(x)\]
Answer: \(148.69\)
(2). Given the function \(f(x) = \sin(2x)\) and using a step size of \(h = 0.1\), find
a) \(f^{\prime}(\displaystyle \frac{\pi}{3})\) using the forward divided difference scheme. Also, find the absolute relative true error.
b) \(f^{\prime}(\displaystyle \frac{\pi}{3})\) using the backward divided difference scheme. Also, find the absolute relative true error.
c) \(f^{\prime}(\displaystyle \frac{\pi}{3})\) using the central divided difference scheme. Also, find the absolute relative true error.
Answer: \(a)\ -1.1660,\ 0.1660\ \ b)\ -0.8207,\ 0.1792\ \ c)\ -0.99334,\ 0.0067\)
(3). Using forward divided difference scheme, find the first derivative of the function \(f(x) = \sin(2x)\) at \(x = \displaystyle \frac{\pi}{3}\) correct within 2 significant digits. Start with a step size of \(h = 0.01\) and keep halving it till you find the answer.
Answer: \(-1.0043,\ \text{abs rel approx error}\ =0.42\%, h=0.0025\)
(4). The velocity of a body is given by
\[v(t) = 20 \ln(120 - 4t), 0 < t < 10\]
where \(t\) is in seconds and \(v\) is in \(\text{m/s}\).
a) What is the exact acceleration at \(t = 2\) s?
b) What is the acceleration at \(t = 2\) s using any divided difference scheme of numerical differentiation with a step size of \(0.25\) s?
c) Use any numerical scheme to find jerk (rate of change of acceleration) at \(t = 2\) s using a step size of \(0.25\) s.
Answer:
\(a)\ -0.7143\ \text{m/s}^2\ \ b)\ -0.7174\ \text{m/s}^2\ \text{(FDD)},\)
\(-0.7111\ \text{m/s}^2\ \text{(BDD)},\ -0.7143\ \text{m/s}^2\ \text{(CDD)}\ \ c)\ -0.0255\ \text{m/s}^2\ \text{using CDD}\)
(5). Using forward divided difference method, the first derivative of a function \(f(x)\) is found at \(x = 0.8\). With a step size of \(0.2\), \(f^{\prime}(0.8) \approx 0.95375\), while with a step size of \(0.1\), \(f^{\prime}(0.8) \approx 0.96851\). Find a better estimate of \(f^{\prime}(0.8)\) with the above information knowing that the order of accuracy of the forward divided difference scheme is \(O\)(step size).
Answer: \(0.98327\)
(6). The error in using central divided difference scheme to find the first derivative of the function, \(f(x)\) is of \(O(h^{2})\), where \(h\) is the step size. If the true error in finding \(f^{\prime}(\alpha)\) with a step size \(h = 0.5\) is \(1.6\), estimate the true error in finding \(f^{\prime}(\alpha)\) with a step size of \(h = 0.125\).
Answer: \(0.1\)
(7). The voltage of a variable power source is given by
\[v(t) = 3\frac{{dc}}{{dt}} + 5c,\]
where \(c\) is the current in amperes, time is in seconds, and \(v\) is the voltage in volts. Find the voltage in volts at \(t = 6\) s if \(c = 5\cos(2t)\).
Answer: \(37.194\ \text{V}\)