Chapter 02.01: Prerequisites to Numerical Differentiation
Learning Objectives
After successful completion of this lesson, you should be able to:
1) recall the exact definition of differentiation
2) derive exact derivatives of a few functions
Introduction
In this lesson, we will review the necessary concepts of differential calculus to learn numerical differentiation. These include the concepts of finding exact derivatives of functions.
The derivative of a function represents the rate of change of a variable with respect to another variable. For example, the velocity of a body is defined as the rate of change of the location of the body with respect to time. The location is the dependent variable, while time is the independent variable. Now, if we measure the rate of change of velocity with respect to time, we get the acceleration of the body. In this case, velocity is the dependent variable, while time is the independent variable.
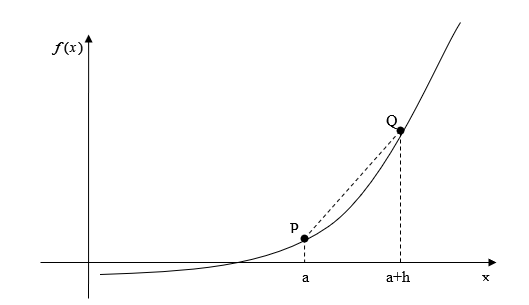
Whenever differentiation is introduced to a student, the two concepts of the secant line and tangent line (Figure 1) are revisited.
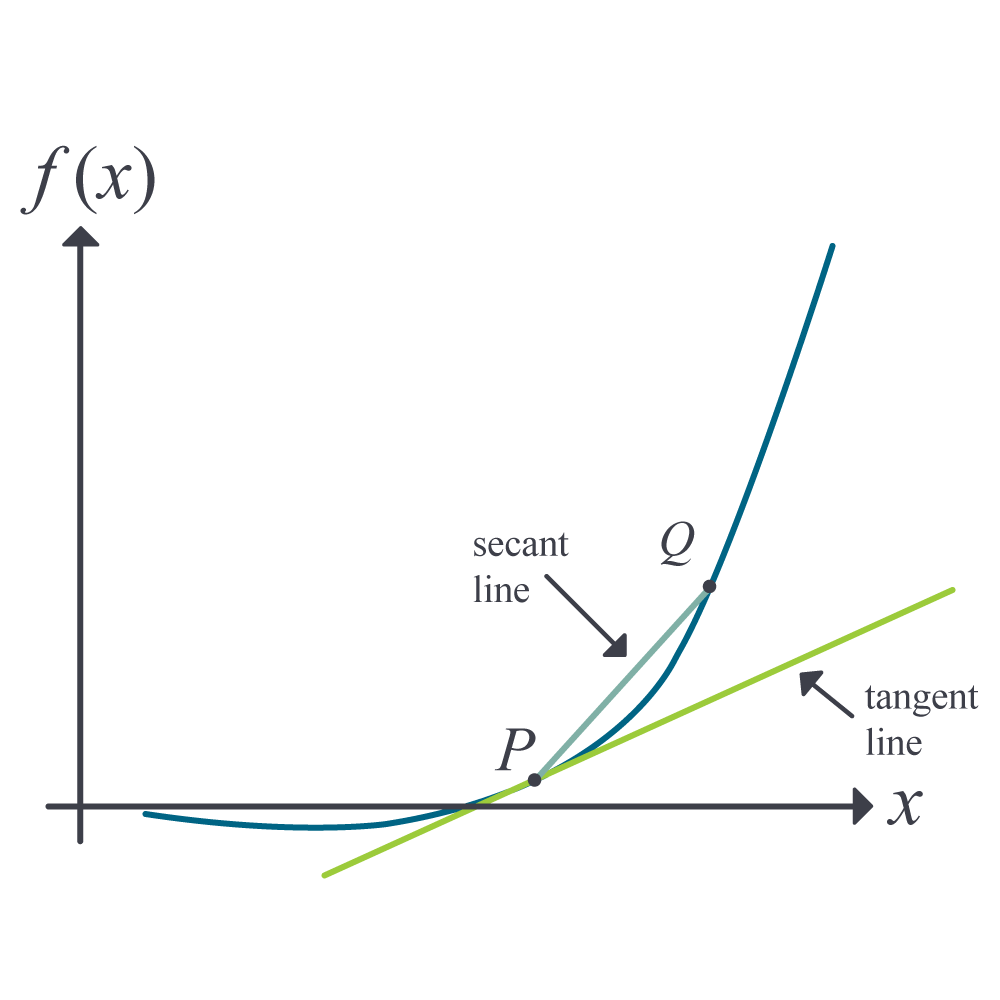
Figure 1: Function curve with tangent and secant lines
Let \(P\) and \(Q\) be two points on the curve, as shown in Figure 1. The secant line is the straight line drawn through \(P\) and \(Q\).
Figure 2: Calculation of the secant line
The slope of the secant line (Figure 2) is then given as
\[\begin{split} m_{{PQ},{secant}} &= \frac{f(a + h) - f(a)}{(a + h) - a}\\ &=\frac{f(a + h) - f(a)}{h}\end{split} \;\;\;\;\;\;\;\;\;\;\;\; (1)\]
As \(Q\) moves closer and closer to \(P\), the limiting portion is called the tangent line. The slope of the tangent line \(m_{PQ,{tangent}}\) then is the limiting value of \(m_{PQ,{secant}}\) from Equation (1) as \(h \rightarrow 0\).
\[m_{{PQ},{tangent}} = \lim_{h \rightarrow 0}\frac{f(a + h) - f(a)}{h} \;\;\;\;\;\;\;\;\;\;\;\; (2)\]
Example 1
Find the slope of the secant line of the curve \(y = 4x^{2}\) between points \((3,36)\) and \((5,100)\).
Solution
The slope of the secant line between \((3,36)\) and \((5,100)\) from Equation (1) is
\[\begin{split} m &=\frac{f(5) - f(3)}{5 - 3}\\ &=\frac{100 - 36}{5 - 3}\\ &= 32\end{split}\]
Example 2
Find the slope of the tangent line of the curve \(y = 4x^{2}\) at point \((3,36)\).
Solution
The slope of the tangent line at \((3,36)\) from Equation (2) is
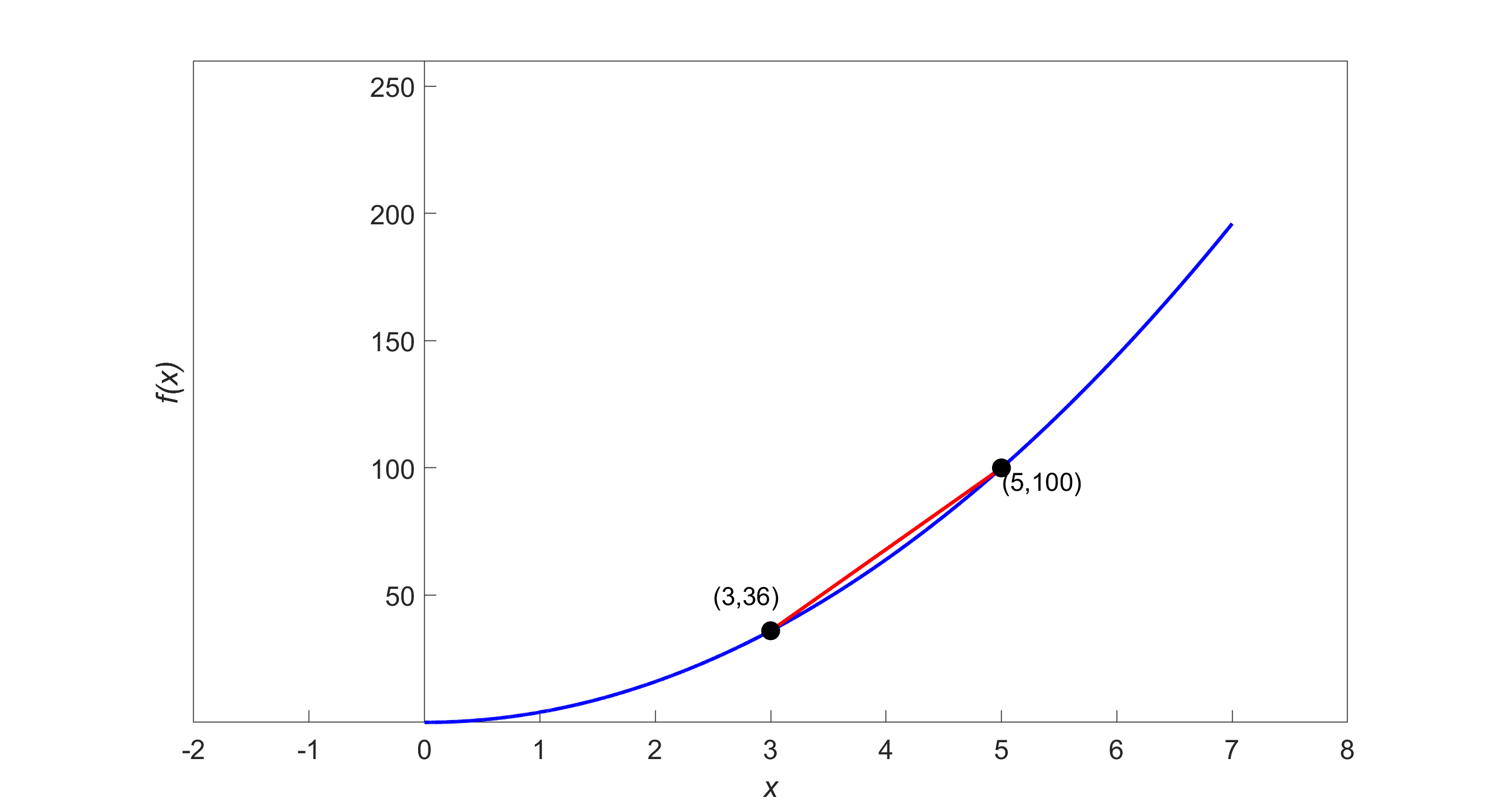
Figure 3: Calculation of the secant line for the function \({y} = {4}{x}^{{2}}\)
\[\begin{split} m &= \lim_{h \rightarrow 0}\frac{f(3 + h) - f(3)}{h}\\ &= \lim_{h \rightarrow 0}\frac{4(3 + h)^{2} - 4(3)^{2}}{h}\\ &= \lim_{h \rightarrow 0}\frac{4(9 + h^{2} + 6h) - 36}{h}\\ &= \lim_{h \rightarrow 0}\frac{36 + 4h^{2} + 24h - 36}{h}\\ &= \lim_{h \rightarrow 0}\frac{h(4h + 24)}{h}\\ &= \lim_{h \rightarrow 0}(4h + 24)\\ &= 24\end{split}\]
Derivative of a Function
Recall from calculus, the derivative of a function \(f(x)\) at \(x = a\) is defined as the slope of the tangent line at \(x = a\)
\[f^{\prime}(a) = \lim_{h \rightarrow 0}\frac{f(a + h) - f(a)}{h} \;\;\;\;\;\;\;\;\;\;\;\; (3)\]
Second Definition of Derivatives
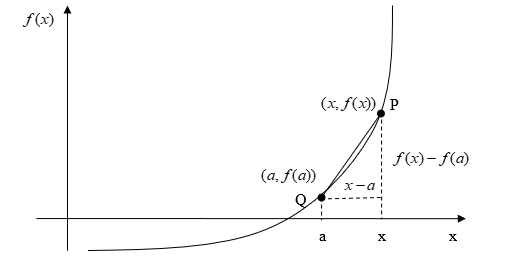
There is another form of the definition of the derivative of a function. The derivative of the function \(f(x)\) at \(x = a\) is defined as
\[f^{\prime}(a) = \lim_{x \rightarrow a}\frac{f(x) - f(a)}{x - a} \;\;\;\;\;\;\;\;\;\;\;\; (4)\]
As \(x \rightarrow a\), the definition is nothing but the slope of the tangent line at \(P\).
Figure 5: Graph showing the second definition of the derivative
Example 4
Find \(f^{\prime}(3)\) if \(f(x) = 4x^{2}\) by using the form
\[f^{\prime}(a) = \lim_{x \rightarrow a}\frac{f(x) - f(a)}{x - a}\]
of the definition of a derivative.
Solution
\[\begin{split} f^{\prime}(3) &= \lim_{x \rightarrow 3}\frac{f(x) - f(3)}{x - 3}\\ &= \lim_{x \rightarrow 3}\frac{4x^{2} - 4(3)^{2}}{x - 3}\\ &= \lim_{x \rightarrow 3}\frac{4x^{2} - 36}{x - 3}\\ &= \lim_{x \rightarrow 3}\frac{4(x^{2} - 9)}{x - 3}\\ &= \lim_{x \rightarrow 3}\frac{4(x - 3)(x + 3)}{x - 3}\\ &= \lim_{x \rightarrow 3}4(x + 3)\\ &= 4(3 + 3) \\ &= 24 \end{split}\]
Higher-Order Derivatives
So far, we have limited our discussion to calculating the first derivative, \(f^{\prime}(x)\) of a function \(f(x)\). What if we are asked to calculate higher-order derivatives of \(f(x)\). A simple example of this is finding the acceleration of a body from a function that gives the location of the body as a function of time. The derivative of the location with respect to time is the velocity of the body, followed by the derivative of velocity with respect to time being the acceleration. Hence, the second derivative of the location function gives the acceleration function of the body.
Example 5
Given \(f(x) = 3x^{3} - 2x - 7\), find the second derivative, \(f^{\prime\prime}(x)\) and the third derivative,\(\ f^{\prime\prime\prime}(x)\). Also, find the value of \(f^{\prime\prime}(2)\) and \(f^{\prime\prime\prime}(2)\).
Solution
Given
\[f(x) = 3x^{3} - 2x - 7\]
we have
\[\begin{split} f^{\prime}(x) &= 3(3x^{2}) - 2\\ &= 9x^{2} - 2\end{split}\]
\[\begin{split} f^{\prime\prime}(x) &= \frac{d}{{dx}}(f^{\prime}(x))\\ &= \frac{d}{{dx}}\left( 9x^{2} - 2 \right)\\ &= 9\left( 2x \right)\\ &= 18x\end{split}\]
\[\begin{split} f\left( 2 \right) &= 18 \times 2\\ &= 36 \end{split}\]
\[\begin{split} f^{\prime\prime\prime}(x) &= \frac{d}{{dx}}(f^{\prime\prime}(x))\\ &= \frac{d}{{dx}}(18x)\\ &= 18\end{split}\]
\[f^{\prime\prime\prime}(2) = 18\]
Other Notations of Derivatives
Derivatives can be denoted in several ways. For the first derivative, the notations include
\[f^{\prime}(x),\ \frac{d}{{dx}}f(x),\ y^{\prime},\dot{y},\ \text{and}\ \frac{{dy}}{{dx}}\]
For the second derivative, the notations include
\[f^{\prime\prime}(x),\ \frac{d^{2}}{{dx}^{2}}f(x),\ y^{\prime\prime},\ \ddot{y},\ \text{and}\ \frac{d^{2}y}{dx^{2}}\]
For the \(n^{th}\) derivative, the notations include
\[f^{(n)}(x),\ \frac{d^{n}}{dx^{n}}f(x),\ y^{(n)},\ \text{and}\ \frac{d^{n}y}{dx^{n}}\]
Learning Objectives
After successful completion of this lesson, you should be able to:
1) find the equation of the tangent line to a function.
Finding equations of a tangent line
One of the numerical methods used to solve a nonlinear equation is called the Newton-Raphson method. This method is based on the prerequisite knowledge of finding the tangent line to a curve at a point. Let us look at an example to illustrate finding the equation of the tangent line to a curve.
Example 1
Find the equation of the line tangent to the function
\[f(x) = x^{3} - 0.165x + 3.993 \times 10^{- 4}\]
\(\text{ at } x = 0.05.\)
Solution
The line tangent is a straight line of the form
\[y = mx + c\]
To find the equation of the tangent line, let us first find the slope \(m\) of the straight line.
\[f^{\prime}(x) = 3x^{2} - 0.165\]
At \(x=0.05\)\[\begin{split} f^{\prime}(0.05) &= 3(0.05)^{2} - 0.165\\ &= - 0.1575 \end{split}\]
Hence\[m = - 0.1575\]
To find the value of the \(y\) -intercept \(c\) of the straight line, we first find the value of the function at \(x = 0.05\).
\[\begin{split} f(0.05) &= (0.05)^{3} - 0.165(0.05) + 3.993 \times 10^{- 4}\\ &= - 0.0077257 \end{split}\]
The tangent line passes through the point \((0.05, - 0.0077257)\), so
\[- 0.0077257 = m(0.05) + c\]
\[- 0.0077257 = - 0.1575(0.05) + c\]
\[c = 0.0001493\]
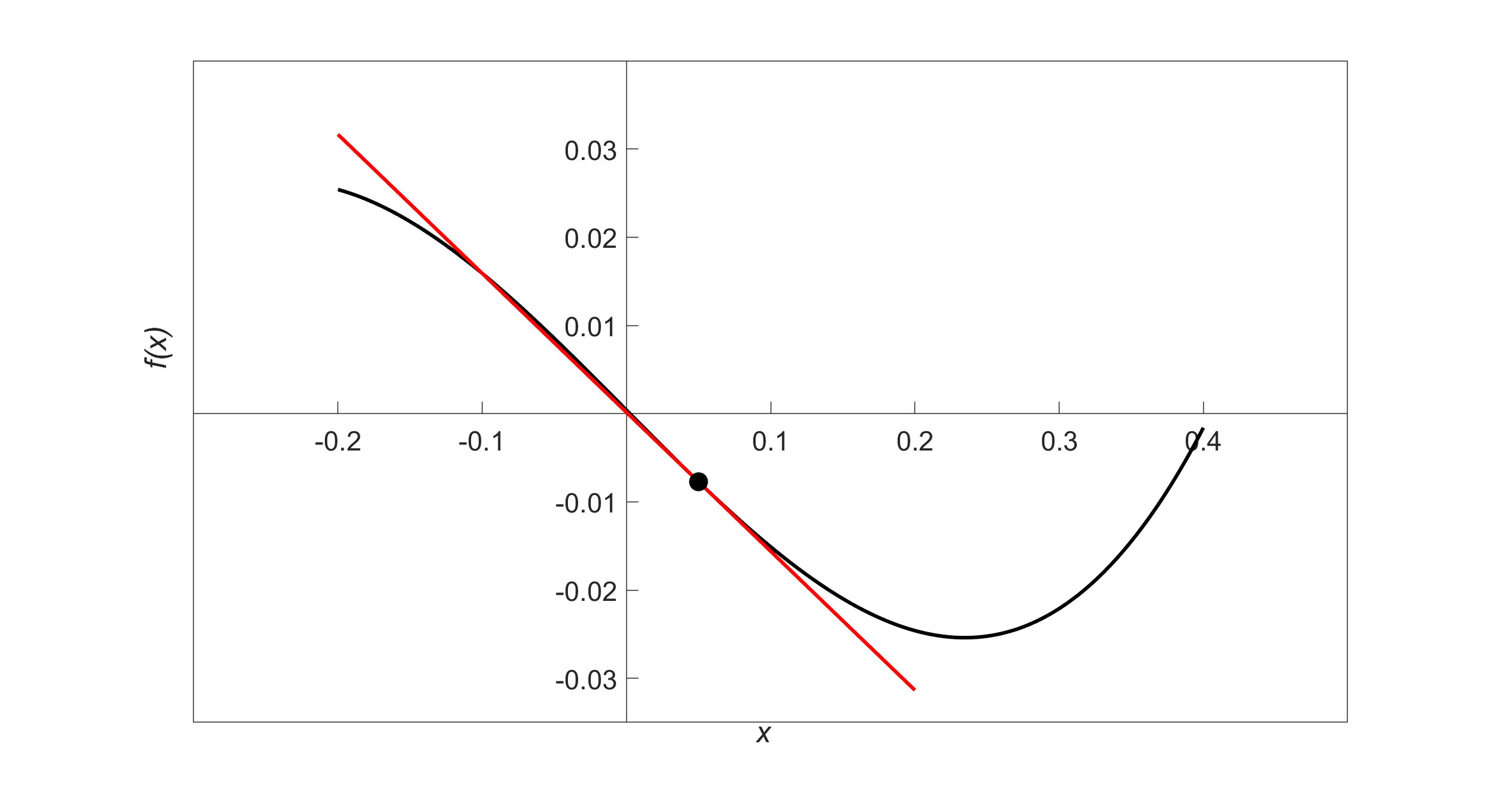
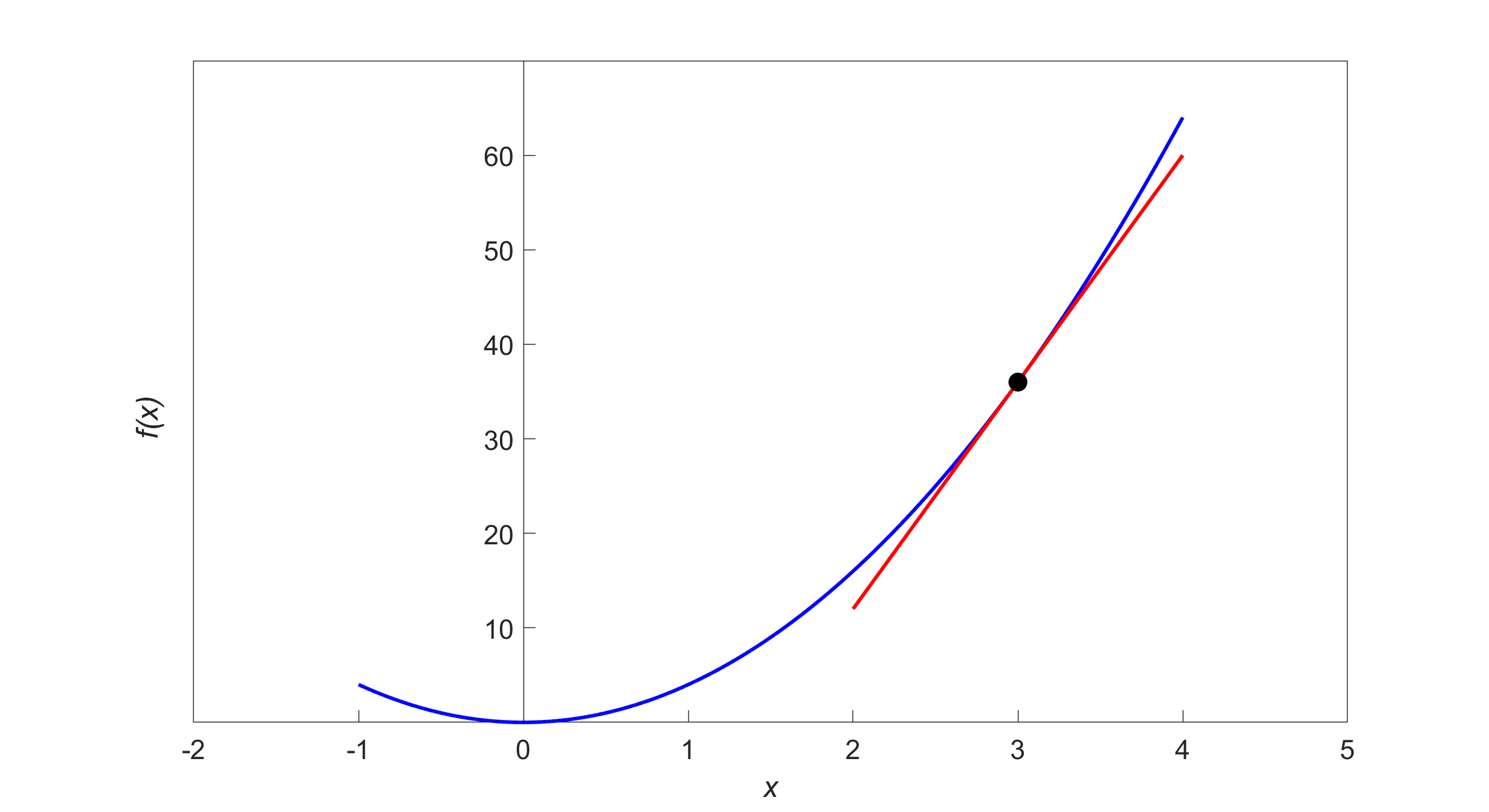
Figure 1 Graph of function \(f(x)\) and the tangent line at \(x = 0.05\).
Hence,
\[\begin{split} y &= mx + c\\ &= - 0.1575x + 0.0001493 \end{split}\]
is the equation of the tangent line.
Learning Objectives
After successful completion of this lesson, you should be able to:
1) state several theorems of differentiation
2) apply the theorems of differentiation in finding the derivatives of complex functions.
Theorems of Differentiation
Several theorems of differentiation are revisited to show how one can find the exact derivative of different functions.
Theorem 1
The derivative of a constant is zero. If \(f(x) = k\), where \(k\) is a constant, \(f^{\prime}(x) = 0\).
Example 1
Find the derivative of \[f(x) = 6.\]
Solution
\[f(x) = 6\]
\[f^{\prime}(x) = 0\]
Theorem 2
The derivative of \(f(x) = x^{n}\), where \(n \neq 0\) is \(f^{\prime}(x) = nx^{n - 1}\).
Example 2
Find the derivative of \[f(x) = x^{6}.\]
Solution
\[f(x) = x^{6}\]
\[\begin{split} f^{\prime}(x) &= 6x^{6 - 1}\\ &= 6x^{5} \end{split}\]
Example 3
Find the derivative of \[f(x) = x^{- 6}.\]
Solution
\[f(x) = x^{- 6}\]
\[\begin{split} f^{\prime}\left( x \right) &= - 6x^{- 6 - 1}\\ &= - 6x^{- 7}\\ &= - \frac{6}{x^{7}} \end{split}\]
Theorem 3
The derivative of \(f(x) = kg(x)\), where \(k\) is a constant is \(f^{\prime}(x) = kg^{\prime}(x)\).
Example 4
Find the derivative of \[f(x) = 10x^{6}.\]
Solution
\[f(x) = 10x^{6}\]
\[\begin{split} f^{\prime}(x) &= \frac{d}{{dx}}(10x^{6})\\ &= 10\frac{d}{{dx}}x^{6}\\ &= 10(6x^{5})\\ &= 60x^{5} \end{split}\]
Theorem 4
The derivative of \(f(x) = u(x) \pm v(x)\) is \(f^{\prime}(x) = u^{\prime}(x) \pm v^{\prime}(x)\).
Example 5
Find the derivative of \[f(x) = 3x^{3} + 8.\]
Solution
\[f\left( x \right)\ = 3x^{3} + 8.\]
\[f^{\prime}\left( x \right) = \frac{d}{{dx}}(3x^{3} + 8)\]
\[\displaystyle \begin{split} f^{\prime}\left( x \right) &= \frac{d}{{dx}}(3x^{3}) + \frac{d}{{dx}}(8)\\ &= 3\frac{d}{{dx}}(x^{3})+0\\ &= 3(3x^{2})\\ &= 9x^{2} \end{split}\]
Theorem 5
The derivative of
\[f(x) = u(x)v(x)\]
is
\[\displaystyle f^{\prime}(x) = u(x)\frac{d}{{dx}}v(x) + v(x)\frac{d}{{dx}}u(x).\ \text{(Product Rule)}\]
Example 6
Find the derivative of \[f(x) = (2x^{2} - 6)(3x^{3} + 8)\]
Solution
Using the product rule as given by Theorem 5 where
\[f(x) = u(x)v(x)\]
\[f^{\prime}(x) = u(x)\frac{d}{{dx}}v(x) + v(x)\frac{d}{{dx}}u(x)\]
\[f(x) = (2x^{2} - 6)(3x^{3} + 8)\]
\[u(x) = 2x^{2} - 6\]
\[v(x) = 3x^{3} + 8\]
Taking the derivative of \(u(x)\),
\[\begin{split} \frac{{du}}{{dx}}\ &= \frac{d}{{dx}}(2x^{2} - 6)\\ &= \frac{d}{{dx}}(2x^{2}) - \frac{d}{{dx}}(6)\\ &= 2\frac{d}{{dx}}(x^{2}) - 0\\ &= 2(2x)\\ &= 4x \end{split}\]
Taking the derivative of \(v(x)\),
\[\begin{split} \frac{{dv}}{{dx}}\ &= \frac{d}{{dx}}(3x^{3} + 8)\\ &= \frac{d}{{dx}}(3x^{3}) + \frac{d}{{dx}}(8)\\ &= 3\frac{d}{{dx}}(x^{3}) + 0\\ &= 3(3x^{2})\\ &= 9x^{2} \end{split}\]
Using the formula for the product rule
\[\begin{split} f^{\prime}(x) &= u(x)\frac{d}{{dx}}v(x) + v(x)\frac{d}{{dx}}u(x)\\ &= (2x^{2} - 6)(9x^{2}) + (3x^{3} + 8)(4x)\\ &= 18x^{4} - 54x^{2} + 12x^{4} + 32x\\ &= 30x^{4} - 54x^{2} + 32x \end{split}\]
Theorem 6
The derivative of
\[f(x) = \frac{u(x)}{v(x)}\]
is
\[f^{\prime}(x) = \frac{v(x)\frac{d}{{dx}}u(x) - u(x)\frac{d}{{dx}}v(x)}{(v(x))^{2}}\ \text{(Quotient Rule)}\]
Example 7
Find the derivative of \[f(x) = \frac{(2x^{2} - 6)}{(3x^{3} + 8)}.\]
Solution
Use the quotient rule of Theorem 6, if
\[f(x) = \frac{u(x)}{v(x)}\]
then
\[f^{\prime}(x) = \frac{v(x)\frac{d}{{dx}}u(x) - u(x)\frac{d}{{dx}}v(x)}{(v(x))^{2}}\]
From
\[f(x) = \frac{(2x^{2} - 6)}{(3x^{3} + 8)}\]
we have
\[u(x) = 2x^{2} - 6\]
\[v(x) = 3x^{3} + 8\]
Taking the derivative of \(u(x)\),
\[\begin{split} \frac{{du}}{{dx}} &= \frac{d}{{dx}}(2x^{2} - 6)\\ &= \frac{d}{{dx}}(2x^{2}) - \frac{d}{{dx}}(6)\\ &= 2\frac{d}{{dx}}(x^{2}) - 0\\ &= 2(2x)\\ &= 4x \end{split}\]
Taking the derivative of \(v(x)\),
\[\begin{split} \frac{{dv}}{{dx}}\ &= \frac{d}{{dx}}(3x^{3} + 8)\\ &= \frac{d}{{dx}}(3x^{3}) + \frac{d}{{dx}}(8)\\ &= 3\frac{d}{{dx}}\left( x^{3} \right) + 0\\ &= 3(3x^{2})\\ &= 9x^{2} \end{split}\]
Using the formula for the quotient rule,
\[\begin{split} f^{\prime}(x) &= \frac{(3x^{3} + 8)(4x) - (2x^{2} - 6)(9x^{2})}{(3x^{3} + 8)^{2}}\\ &= \frac{12x^{4} + 32x - 18x^{4} + 54x^{2}}{9x^{6} + 48x^{3} + 64}\\ &= \frac{- 6x^{4} + 54x^{2} + 32x}{9x^{6} + 48x^{3} + 64} \end{split}\]
Table of Derivatives
| \(f(x)\) | \(f^{\prime}(x)\) |
|---|---|
| \(x^n,\ n\neq0\) | \(nx^{n-1}\) |
| \(kx^n,\ n\neq 0\) | \(knx^{n-1}\) |
| \(\sin(x)\) | \(\cos(x)\) |
| \(\cos(x)\) | \(-\sin(x)\) |
| \(\tan(x)\) | \(\sec^2(x)\) |
| \(\sinh(x)\) | \(\cosh(x)\) |
| \(\cosh(x)\) | \(\sinh(x)\) |
| \(\tanh(x)\) | \(1-\tanh^2(x)\) |
| \(\sin^{-1}(x)\) | \(\displaystyle \frac{1}{\sqrt{1-x^2}}\) |
| \(\cos^{-1}(x)\) | \(\displaystyle \frac{-1}{\sqrt{1-x^2}}\) |
| \(\tan^{-1}(x)\) | \(\displaystyle \frac{1}{{1+x^2}}\) |
| \(\csc(x)\) | \(-\csc(x)\cot(x)\) |
| \(\sec(x)\) | \(\sec(x)\tan(x)\) |
| \(\cot(x)\) | \(-csc^2(x)\) |
| \(csch(x)\) | \(-\coth(x)csch(x)\) |
| \(sech(x)\) | \(-\tanh(x)sech(x)\) |
| \(\coth(x)\) | \(1-\coth^2(x)\) |
| \(csc^{-1}(x)\) | \(\displaystyle -\frac{|x|}{x^2\sqrt{x^2-1}}\) |
| \(\sec^{-1}(x)\) | \(\displaystyle \frac{|x|}{x^2\sqrt{x^2-1}}\) |
| \(\cot^{-1}(x)\) | \(\displaystyle \frac{-1}{1+x^2}\) |
| \(a^x\) | \(\ln(a)a^x\) |
| \(\ln(x)\) | \(\displaystyle \frac{1}{x}\) |
| \(\log_a(x)\) | \(\displaystyle \frac{1}{x\ln(a)}\) |
| \(e^x\) | \(e^x\) |
Chain Rule of Differentiation
Sometimes functions that need to be differentiated do not fall in the form of simple functions or the forms described previously. Such functions can be differentiated using the chain rule if they are of the form \(f(g(x))\). The chain rule states
\[\frac{d}{{dx}}(f(g(x)) = f^{\prime}(g(x))g^{\prime}(x)\]
For example, to find \(f^{\prime}(x)\) of \(f(x) = (3x^{2} - 2x)^{4}\), one could use the chain rule.
\[g(x) = (3x^{2} - 2x)\]
\[g^{\prime}(x) = 6x - 2\]
\[f^{\prime}(g(x)) = 4(g(x))^{3}\]
\[\frac{d}{{dx}}((3x^{2} - 2x)^{4}) = 4(3x^{2} - 2x)^{3}(6x - 2)\]
Implicit Differentiation
Sometimes, the function to be differentiated is not given explicitly as an expression of the independent variable. In such cases, how do we find the derivatives? We will discuss this via examples.
Example 8
Find \[\frac{{dy}}{{dx}} \text{ if } x^{2} + y^{2} = 2xy\]
Solution
\[x^{2} + y^{2} = 2xy\]
\[\frac{d}{{dx}}(x^{2} + y^{2}) = \frac{d}{{dx}}(2xy)\]
\[\frac{d}{{dx}}(x^{2}) + \frac{d}{{dx}}(y^{2}) = \frac{d}{{dx}}(2xy)\]
\[2x + 2y\frac{{dy}}{{dx}} = 2x\frac{{dy}}{{dx}} + 2y\]
\[2y\frac{{dy}}{{dx}} - 2x\frac{{dy}}{{dx}} = 2y - 2x\]
\[(2y - 2x)\frac{{dy}}{{dx}} = 2y - 2x\]
\[\frac{{dy}}{{dx}} = \frac{2y - 2x}{2y - 2x}\]
\[\frac{{dy}}{{dx}} = 1\]
Example 9
If \(x^{2} - xy + y^{2} = 5\), find the value of \(y^{\prime}\).
Solution
\[x^2-xy+y^2 =5\]
\[\frac{d}{dx}(x^2-xy+y^2) =5\]
\[\frac{d}{dx}(x^2)-\frac{d}{dx}(xy)+\frac{d}{dx}(y^2) =0\]
\[2x - x\frac{dy}{dx} -y +2y\frac{dy}{dx} =0\]
\[(-x+2y)\frac{dy}{dx} = -2x+y\]
\[\frac{dy}{dx} = \frac{y-2x}{2y-x}\]
\[y^{\prime} = \frac{y-2x}{2y-x}\]
Learning Objectives
After successful completion of this lesson, you should be able to:
1) find the minimum and maximum of a function of one variable.
Finding maximum and minimum of a function
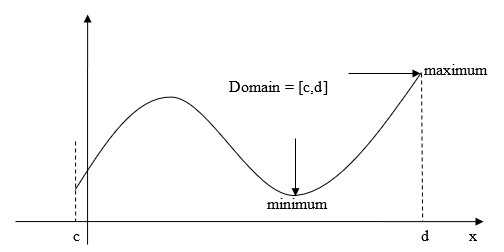
The knowledge of the first derivative and second derivative of a function is used to find the minimum and maximum of a function. First, let us define what the maximum and minimum of a function are. Let \(f(x)\) be a function in domain \(D\), then
\(f(a)\) is the maximum of the function if \(f(a) \geq f(x)\) for all values of \(x\) in the domain \(D\).
\(f(a)\) is the minimum of the function if \(f(a) \leq f(x)\) for all values of \(x\) in the domain \(D\).
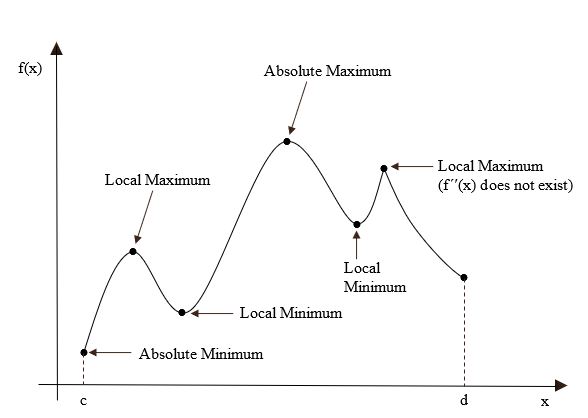
The minimum and maximum of a function are also the critical values of a function.
An extreme value can also occur in the interval \(\lbrack c,d\rbrack\) at
1) endpoints \(x = c,x = d,\)
2) a point in \(\lbrack c,d\rbrack\) where \(f^{\prime}(x) = 0\).
3) a point in \(\lbrack c,d\rbrack\) where \(f^{\prime}(x)\) does not exist.
These critical points can be the local maxima and minima of the function (See Figure 2).
Example 1
Find the minimum and maximum value of \(f(x) = x^{2} - 2x - 5\) in the interval \(\lbrack 0,5\rbrack\).
Figure 1. Graph illustrating the concepts of maximum and minimum
Figure 2. The plot showing critical points of \(f(x)\) in \(\lbrack c,d\rbrack\)
Solution
\[f(x) = x^{2} - 2x - 5\]
\[f^{\prime}(x) = 2x - 2\]
\[f^{\prime}(x) = 0\ \text{at}\ x = 1.\]
\[f^{\prime}(x)\ \text{exists everywhere in}\ \lbrack 0,5\rbrack.\]
So, the critical points are \(x = 0,x = 1,x = 5\).
\[f(0) = (0)^{2} - 2(0) - 5\ = - 5\]
\[f(1) = (1)^{2} - 2(1) - 5\ = - 6\]
\[f(5) = (5)^{2} - 2(5) - 5\ = 10\]
Hence, the minimum value of \(f(x)\) occurs at \(x = 1\), and the maximum value occurs at \(x = 5\).
Figure 3. Maximum and minimum values of \(f(x) = x^2-2x-5\) over the interval \(\lbrack 0,5\rbrack\)
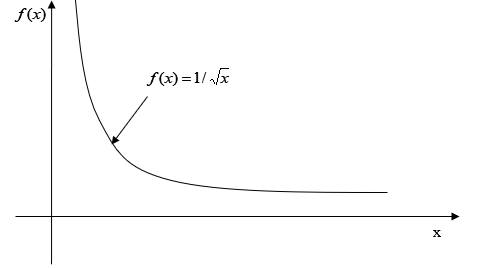
Figure 4 shows an example of a function that has no minimum or maximum value in the domain \(\ (0,\infty)\).
Figure 4. Function that has no maximum or minimum in an open interval.
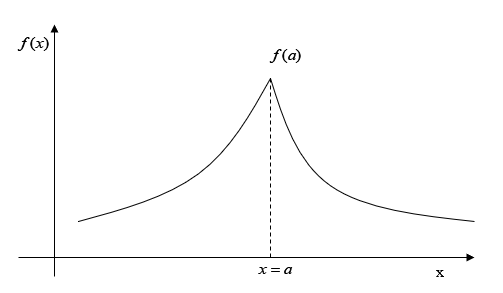
Figure 5 shows the maximum of the function occurring at a singular point. The function \(f(x)\) has a sharp corner at \(x = a\), where \(f ^{\prime}(x)\) does not exist.
Figure 5. Graph demonstrates the concept of a singular point with discontinuous slope at \(x=a\)
Example 2
Find the maximum and minimum of \(f(x) = 2x\) in the interval \(\lbrack 0,5\rbrack\).
Solution
\[f(x) = 2x\]
\[f^{\prime}(x) = 2\]
\[f^{\prime}(x) \neq 0\ \text{on}\ \lbrack 0,5\rbrack.\]
So the critical points are \(x = 0\) and \(x = 5\).
\[f(x) = 2x\]
\[f(0) = 2(0) = 0\]
\[f(5) = 2(5) = 10\]
So the minimum value of \(f(x) = 2x\) is at \(x = 0\), and the maximum value is at \(x = 5\).
The point(s) where the second derivative of a function becomes zero is a way to know whether the critical point found in the first derivative test is a local minimum or maximum. Let \(f(x)\) be a function in the interval \((c,d)\) and \(f(a) = 0\).
\(f(a)\) is a local maximum of the function if \(f^{\prime\prime}(a) < 0\).
\(f(a)\) is a local minimum of the function if \(f^{\prime\prime}(a) > 0\).
If \(f^{\prime\prime}(a) = 0\), then the second derivative does not offer any insight into the local maxima or minima.
Example 3
Remember Example 1 where we found \(f^\prime(x) = 0\) at \(x = 1\) for \(f(x) = x^{2} - 2x - 5\) in the interval \(\lbrack 0,5\rbrack\). Is \(x = 1\) a local maxima or minima of the function?
Solution
\[f(x) = x^{2} - 2x - 5\]
\[f^{\prime}(x) = 2x - 2\]
\[f^{\prime}(x) = 0\ \text{at}\ x = 1\]
\[{f^{\prime\prime}(x) = 2 }\] \[{f^{\prime\prime}(1) = 2 > 0}\]
So the \(f(1)\) is the local minimum of the function.
Applications of Derivatives
Below are some examples to show real-life applications of differentiation.
Example 4
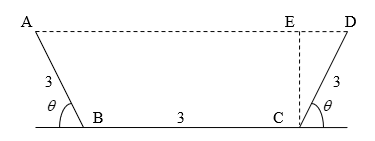
A rain gutter cross-section is shown below.
Figure 6. Gutter dimensions for example 4
What angle of \(\theta\) would make the cross-sectional area of ABCD maximum? Note that common sense or intuition may lead us to believe that \(\displaystyle \theta = \pi/4\) would maximize the cross-sectional area of ABCD. Question your intuition.
Solution
\[Area =\frac{{1}}{{2}}{(}\overline{{{BC}}}{+}\overline{{{AD}}}{) \times}\overline{{{CE}}}\]
\[\begin{split} \overline{{CE}} &= \overline{{CD}}sin(\theta)\\ &= 3sin(\theta) \end{split}\]
\[\overline{{BC}} = 3\]
\[\overline{{AD}} = \overline{{BC}} + \overline{{CD}}\cos(\theta) + \overline{{AB}}cos(\theta)\]
\[\overline{{AD}} = 3 + 3cos(\theta) + 3cos(\theta)\]
\[\overline{{AD}} = 3 + 6cos(\theta)\]
\[\begin{split} Area &= \frac{1}{2}(3 + 3 + 6cos(\theta))(3sin(\theta))\\ &= 9sin(\theta) + 9sin(\theta)cos(\theta)\\ &= 9sin(\theta) + \frac{9}{2}sin(2\theta) \end{split}\]
\[\displaystyle \begin{split} \frac{{dA}}{{d\theta}} &= 9cos(\theta) + \frac{9}{2} \times 2cos(2\theta)\\ &= 9cos(\theta) + 9cos(2\theta) \end{split}\]
When is \(\displaystyle \frac{{dA}}{{d\theta}} = 0\)?
\[9cos(\theta) + 9cos(2\theta) = 0\]
\[\theta = \frac{\pi}{3}\]
The angle at which the area is maximum is \(\theta = 60{^\circ}\).
\[\begin{split} {Area}\left( \frac{\pi}{3} \right) &= 9sin\left( \frac{\pi}{3} \right) + \frac{9}{2}\sin\left( 2\left( \frac{\pi}{3} \right) \right)\\ &= 9\left( \frac{\sqrt{3}}{2} \right) + \frac{9}{2}\left( \frac{\sqrt{3}}{2} \right)\\ &= \frac{27}{4}\sqrt{3} \end{split}\]
For the interval of \(\theta = \lbrack 0,\pi\rbrack\), the area at the endpoints is
\[Area(0) = 0\]
\[Area(\pi) = 0\]
Example 5
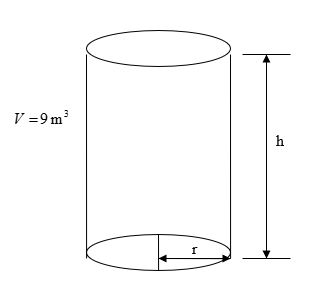
A classic example of the application of differentiation is to find the dimensions of a circular cylinder for a specific volume but which uses the least amount of material. Do this classic problem for a volume of \(9m^{3}\).
Solution
The total surface area, \(A\) of the cylinder is
\[\begin{split} A &= \text{top surface} + \text{side surface} + \text{bottom surface}\\ &= \pi r^{2} + 2\pi rh + \pi r^{2}\\ &= 2\pi r^{2} + 2\pi rh \end{split}\]
The volume, \(V\) of the cylinder is
\[V = \pi r^{2}h\]
since
\[V = 9 m^{3}.\]
We can write
\[{9 = \pi r^{2}h }\]
\[{h = \frac{9}{\pi r^{2}}}\]
This gives the surface area just in terms of \(r\) as
\[\begin{split} A &= 2\pi r^{2} + 2\pi r\left( \frac{9}{\pi r^{2}} \right)\\ &= 2\pi r^{2} + \frac{18}{r}\\ &= 2\pi r^{2} + 18r^{- 1} \end{split}\]
Figure 7. Cylinder Drawing for example 5
To find the minimum, take the first derivative of \(A\) with respect to \(r\) as
\[\begin{split} \frac{{dA}}{{dr}} &= 4\pi r + 18( - 1)r^{- 2}\\ &= 4\pi r - \frac{18}{r^{2}} \end{split}\]
Solving for
\[\displaystyle \frac{{dA}}{{dr}} = 0,\]
\[\displaystyle 4\pi r - \frac{18}{r^{2}} = 0\]
\[4\pi r^{3} - 18 = 0\]
\[r^{3} = \frac{18}{4\pi}\]
\[\begin{split} r &= \left( \frac{18}{4\pi} \right)^{\frac{1}{3}}\\ &= 1.12725m \end{split}\]
Since
\[\displaystyle h = \frac{9}{\pi r^{2}},\]
\[\displaystyle \begin{split} h &= \frac{9}{\pi(1.12725)^{2}}\\ &= 2.25450m \end{split}\]
But does this value of \(r\) correspond to a minimum?
\[\begin{split} \frac{d^{2}A}{dr^{2}} &= 4\pi - 18( - 2)r^{- 3}\\ &= 4\pi + \frac{36}{r^{3}}\\ &= 4\pi + \frac{36}{1.12725}\\ &= 44.5025 \end{split}\]
This value \(\displaystyle \frac{d^{2}A}{dr^{2}} > 0\) for \(r = 1.12725m\). As per the second derivative test, \(r = 1.12725m\) corresponds to a minimum. The value of \(r = 1.12725m\) also corresponds to the absolute minimum as \(\frac{{dA}}{{dr}}=0\) has only one real solution, and that \(A(r)\) is a continuous function of \(r\).
Multiple Choice Test
(1). The definition of the first derivative of a function \(f(x)\) is
(A) \(\displaystyle f^{\prime}(x) = \frac{f(x + \Delta x) + f(x)}{{\Delta x}}\)
(B) \(\displaystyle f^{\prime}(x) = \frac{f(x + \Delta x) - f(x)}{{\Delta x}}\)
(C) \(\displaystyle f^{\prime}(x) = \lim_{\Delta x \rightarrow 0} \frac{f(x + \Delta x) + f(x)}{{\Delta x}}\)
(D) \(\displaystyle f^{\prime}(x) = \lim_{\Delta x \rightarrow 0}\frac{f(x + \Delta x) - f(x)}{{\Delta x}}\)
(2). Given \(y = 5e^{3x} + \sin x,\) \(\displaystyle \frac{{dy}}{{dx}}\) is
(A) \(5e^{3x} + \cos x\)
(B) \(15e^{3x} + \cos x\)
(C) \(15e^{3x} - \cos x\)
(D) \(2.666e^{3x} - \cos x\)
(3). Given \(y = \sin 2x,\displaystyle \frac{{dy}}{{dx}}\) at \(x = 3\) is most nearly
(A) \(0.9600\)
(B) \(0.9945\)
(C) \(1.920\)
(D) \(1.989\)
(4). Given \(y = x^{3}\ln x,\displaystyle \frac{{dy}}{{dx}}\) is
(A) \(3x^{2}\ln x\)
(B) \(3x^{2}\ln x + x^{2}\)
(C) \(x^{2}\)
(D) \(3x\)
(5). The velocity of a body as a function of time is given as \(v\left( t \right) = 5e^{- 2t} + 4\), where \(t\) is in seconds, and \(v\) is in m/s. The acceleration in \({m/}{s}^{2}\) at \(t = 0.6\) s is
(A) \(-3.012\)
(B) \(5.506\)
(C) \(4.147\)
(D) \(-10.00\)
(6). If \(x^{2} + 2xy = y^{2}\), then \(\displaystyle \frac{{dy}}{{dx}}\) is
(A) \(\displaystyle \frac{x + y}{y - x}\)
(B) \(2x + 2y\)
(C) \(\displaystyle \frac{x + 1}{y}\)
(D) \(- x\)
For complete solution, go to
http://nm.mathforcollege.com/mcquizzes/02dif/quiz_02dif_background_solution.pdf
Problem Set
(1). Find the slope of the secant line for \[y = 4x^{2} + 6x - 7\] if the secant is drawn between points at \(x = 3\) and \(x = 5\).
Answer: \(38\)
(2). Find the slope of the tangent line to \[y = 4x^{2} + 6x - 7\]
at \(x = 3\).
Answer: \(30\)
(3). Find the derivative of \[y = 4x^{2} + 6x - 7\] at \(x = 3\).
Answer: \(30\)
(4). Find the derivative of \[y = \frac{1}{5x - 3}\]
at \(x = 2\).
Answer: \(\displaystyle -\frac{5}{\left(5x-3\right)^2}\)
(5). Find the derivative of \[y = \frac{2x - 6}{5x - 9}\] at \(x = 4\).
Answer: \(0.099174\)
(6). Find the derivative of \[y = (2x - 6)(5x - 9)\] at \(x = 4\).
Answer: \(32\)
(7). Find \(y^{\prime\prime}\) at \(x = 2\), given \[y = 4x^{2} + 6x - 7\]
Answer: \(8\)
(8). Find \(y^{\prime\prime}\) at \(x = 4\), given \[y = \frac{2x - 6}{5x - 9}\]
Answer: \(-0.090158\)
(9). Show that \[\left| \frac{y^{\prime\prime}}{(1 + (y^{\prime})^{2})^{\frac{3}{2}}} \right| = \frac{1}{r}\] if \[x^{2} + y^{2} = r^{2}.\]
(10). Given \[x^{2}y + xy^{2} + y^{2} = 5\]
find \(y^{\prime}\) and \(y^{\prime\prime}\).
Answer: \(\displaystyle y^\prime =\frac{-y^2-2xy}{x^2+2yx+2y}\)
\(\displaystyle y^{\prime\prime} =\frac{2y\left(2x^4+6x^3y+6x^2y^2+3xy^3-4y^2+3y^3\right)}{\left(x^2+2xy+2y\right)^2}\)
(11). For \[f(x) = x^{2} + 3x\] find the critical points, and the minimum and maximum value in the domain \(\lbrack - 5,1\rbrack\).
Answer: So the critical points are \(x=-5,\ x=-1.5,\ x=1\).
The maximum is at \(x=-5\), minimum is at \(x=-1.5\)
(12). Find the optimum angle \(\theta\) for maximizing the cross-section of the gutter given in the figure below. The total length of the sheet from which the gutter is made is \(9^{\prime\prime}\), where \(BC =3 ^{\prime\prime}\).
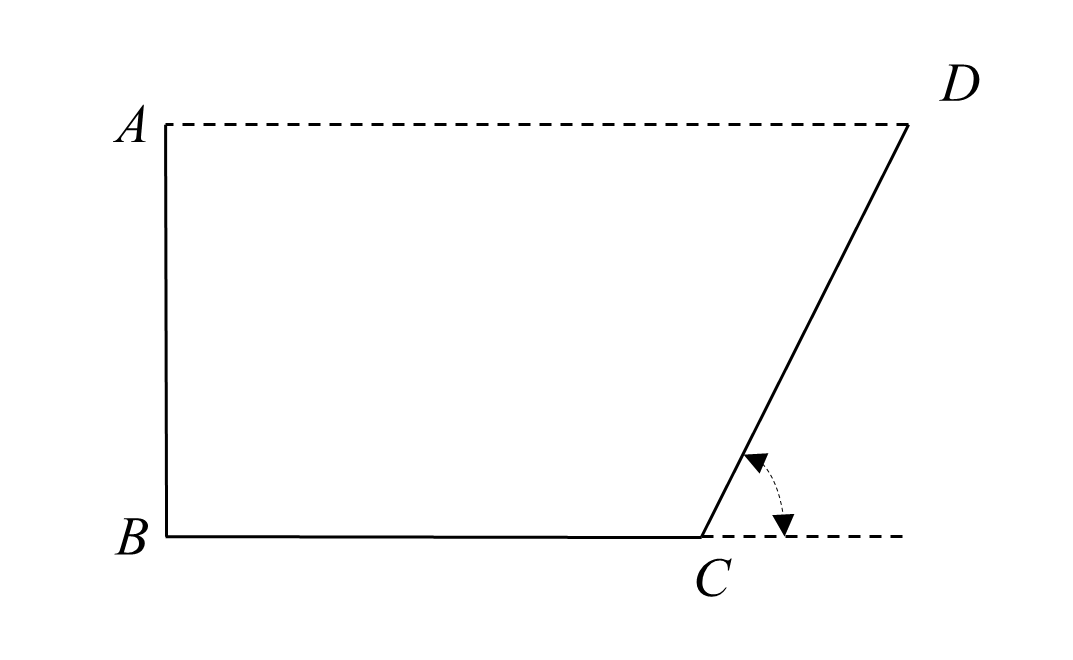
Answer: \(10.667\)
(13). A rectangle is inscribed in a semi-circle of radius \(2\) m. If the area of the rectangle is to be maximized, find the dimensions of the rectangle.
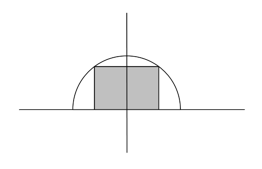
Answer: \(2.828 \times1.414\)
.PNG)