Chapter 03.07: Newton-Raphson Method For Solving Simultaneous Nonlinear Equations
Learning Objectives
After reading this chapter, you should be able to:
1) derive the Newton-Raphson method formula for simultaneous nonlinear equations,
2) develop the algorithm of the Newton-Raphson method for solving simultaneous nonlinear equations,
3) use the Newton-Raphson method to solve a set of simultaneous nonlinear equations,
4) model a real-life problem that results in a set of simultaneous nonlinear equations.
Introduction
Several physical systems result in a mathematical model in terms of simultaneous nonlinear equations. A set of such equations can be written as
\[\begin{split} &f_{1}(x_{1},x_{2},...,x_{n}) = 0\\ &\text{...}\\ &\text{...}\\ &f_{n}(x_{1},x_{2},...,x_{n}) = 0 \end{split}\;\;\;\;\;\;\; (1)\]
The solution to these simultaneous nonlinear equations are values of \(x_{1},x_{2},...,x_{n}\) which satisfy all the above \(n\) equations. The number of set of solutions to these equations could be none, unique, more than one but finite, or infinite. In this chapter, we use the Newton-Raphson method to solve these equations.
The Newton-Raphson method of solving a single nonlinear equation, \(f(x) = 0\), can be derived using first-order Taylor series (first two terms of Taylor series) and are given by
\[f(x_{i + 1}) = f(x_{i}) + f^{\prime}(x_{i})(x_{i + 1} - x_{i})\;\;\;\;\;\;\; (2)\]
where
\[x_{i} = \text{previous estimate of root}\]
\[x_{i + 1} = \text{present estimate of root}\]
Since we are looking for \(x_{i + 1}\)where \(f(x_{i + 1})\) becomes zero, Equation (2) can be re-written as
\[0 = f(x_{i}) + f^{\prime}(x_{i})(x_{i + 1} - x_{i})\]
and then as a recursive formula as
\[x_{i + 1} = x_{i} - \frac{f(x_{i})}{f^{\prime}(x_{i})}\;\;\;\;\;\;\; (3)\]
Derivation
Now how do we extend the same to simultaneous nonlinear equations? For sake of simplicity, let us limit the number of nonlinear equations to two as
\[u(x,y) = 0\;\;\;\;\;\;\; (4a)\]
\[v(x,y) = 0\;\;\;\;\;\;\; (4b)\]
The first order Taylor-series for nonlinear equation is (4a) & (4b) are
\[u(x_{i + 1},y_{i + 1}) = u(x_{i},y_{i}) + \left.\frac{\partial u}{\partial x}\right|_{x_{i},y_{i}} (x_{i + 1} - x_{i}) + \left. \frac{\partial u}{\partial y}\right|_{x_{i},y_{i}} (y_{i + 1} - y_{i})\;\;\;\;\;\;\; (5a)\]
\[v(x_{i + 1},y_{i + 1}) = v(x_{i},y_{i}) + \left. \frac{\partial v}{\partial x}\right|_{x_{i},y_{i}} (x_{i + 1} - x_{i}) + \left.\frac{\partial v}{\partial y}\right|_{x_{i},y_{i}}(y_{i + 1} - y_{i})\;\;\;\;\;\;\; (5b)\]
We are looking for \((x_{i + 1},y_{i + 1})\) where \(u(x_{i + 1},y_{i + 1})\) and \(v(x_{i + 1},y_{i + 1})\) are zero. Hence
\[0 = u(x_{i},y_{i}) + \left.\frac{\partial u}{\partial x}\right|_{x_{i},y_{i}} (x_{i + 1} - x_{i}) + \left.\frac{\partial u}{\partial y}\right|_{x_{i},y_{i}}(y_{i + 1} - y_{i}) \;\;\;\;\;\;\;(6a)\]
\[0 = v(x_{i},y_{i}) + \left.\frac{\partial v}{\partial x}\right|_{x_{i},y_{i}} (x_{i + 1} - x_{i}) + \left.\frac{\partial v}{\partial y}\right|_{x_{i},y_{i}} (y_{i + 1} - y_{i})\;\;\;\;\;\;\; (6b)\]
Writing
\[x_{i + 1} - x_{i} = \Delta x\;\;\;\;\;\;\; (7a)\]
\[y_{i + 1} - y_{i} = \Delta y\;\;\;\;\;\;\; (7b)\]
we get
\[0 = u(x_{i},y_{i}) + \left.\frac{\partial u}{\partial x}\right|_{x_{i},y_{i}} \Delta x + \left.\frac{\partial u}{\partial y}\right|_{x_{i},y_{i}} \Delta y\;\;\;\;\;\;\; (8a)\]
\[0 = v(x_{i},y_{i}) + \left.\frac{\partial v}{\partial x}\right|_{x_{i},y_{i}} \Delta x + \left.\frac{\partial v}{\partial y}\right|_{x_{i},y_{i}} \Delta y\;\;\;\;\;\;\; (8b)\]
Rewriting Equations (8a) and (8b)
\[\left.\frac{\partial u}{\partial x}\right| x_{i},y_{i} \Delta x + \left.\frac{\partial u}{\partial y}\right|_{x_{i},y_{i}} \Delta y = - u(x_{i},y_{i})\;\;\;\;\;\;\; (9a)\]
\[\left.\frac{\partial v}{\partial x}\right| x_{i},y_{i} \Delta x + \left.\frac{\partial v}{\partial y}\right|_{x_{i},y_{i}} \Delta y = - v(x_{i},y_{i})\;\;\;\;\;\;\; (9b)\]
and then in the matrix form
\[\begin{bmatrix} \displaystyle\left.\frac{\partial u}{\partial x}\right|_{x_i,y_i} & \displaystyle\left.\frac{\partial u}{\partial y}\right|_{x_i,y_i}\\ \displaystyle\left.\frac{\partial v}{\partial x}\right|_{x_i,y_i} & \displaystyle\left.\frac{\partial v}{\partial y}\right|_{x_i,y_i} \end{bmatrix} \begin{bmatrix} \Delta x \\ \Delta y \\ \end{bmatrix} = \begin{bmatrix} - u(x_{i},y_{i}) \\ - v(x_{i},y_{i}) \\ \end{bmatrix}\;\;\;\;\;\;\; (10)\]
Solving Equation (10) would give us \(\Delta x\) and \(\Delta y\). Since the previous estimate of the root is \((x_{i},y_{i})\), one can find from Equation (7)
\[x_{i + 1} = x_{i} + \Delta x\;\;\;\;\;\;\; (11a)\]
\[y_{i + 1} = y_{i} + \Delta y\;\;\;\;\;\;\; (11b)\]
This process is repeated till one obtains the root of the equation within a prespecified tolerance,\(\varepsilon_{s}\) such that
\[\left| \varepsilon_{a} \right|_{x} = \left| \frac{x_{i + 1} - x_{i}}{x_{i + 1}} \right| \times 100 < \varepsilon_{s}\]
\[\left| \varepsilon_{a} \right|_{y} = \left| \frac{y_{i + 1} - y_{i}}{y_{i + 1}} \right| \times 100 < \varepsilon_{s}\]
Example 1
Find the roots of the simultaneous nonlinear equations
\[\begin{matrix} x^{2} + y^{2} = 50 \\ x - y = 10 \\ \end{matrix}\]
Use an initial guess of \((x,y) = (2, - 4)\). Conduct two iterations.
Solution
First put the equations in the form
\[u(x,y) = 0\]
\[v(x,y) = 0\]
to give
\[u(x,y) = x^{2} + y^{2} - 50 = 0\] \[v(x,y) = x - y - 10 = 0\]
Now
\[\frac{\partial u}{\partial x} = 2x\]
\[\frac{\partial u}{\partial y} = 2y\]
\[\frac{\partial v}{\partial x} = 1\]
\[\frac{\partial v}{\partial y} = - 1\]
Hence from Equation (10)
\[\begin{bmatrix} \displaystyle\left.\frac{\partial u}{\partial x}\right|_{x_i,y_i} & \displaystyle\left.\frac{\partial u}{\partial y}\right|_{x_i,y_i}\\ \displaystyle\left.\frac{\partial v}{\partial x}\right|_{x_i,y_i} & \displaystyle\left.\frac{\partial v}{\partial y}\right|_{x_i,y_i} \end{bmatrix} \begin{bmatrix} \Delta x \\ \vdots \\ \Delta y \\ \end{bmatrix} = \begin{bmatrix} - u(x_{i},y_{i}) \\ \vdots \\ - v(x_{i},y_{i}) \\ \end{bmatrix}\]
\[\begin{bmatrix} 2x_{i} & 2y_{i} \\ 1 & - 1 \\ \end{bmatrix}\begin{bmatrix} \Delta x \\ \Delta y \\ \end{bmatrix} = \begin{bmatrix} - {x_{i}}^{2} - y_{i}^{2} + 50 \\ - x_{i} + y_{i} + 10 \\ \end{bmatrix}\]
Iteration 1
The initial guess
\[(x_{i},y_{i}) = (2, - 4)\]
Hence
\[\begin{bmatrix} 2(2) & 2( - 4) \\ 1 & - 1 \\ \end{bmatrix}\begin{bmatrix} \Delta x \\ \Delta y \\ \end{bmatrix} = \begin{bmatrix} - (2)^{2} - ( - 4)^{2} + 50 \\ - (2) + ( - 4) + 10 \\ \end{bmatrix}\]
\[\begin{bmatrix} 4 & - 8 \\ 1 & - 1 \\ \end{bmatrix}\begin{bmatrix} \Delta x \\ \Delta y \\ \end{bmatrix} = \begin{bmatrix} 30 \\ 4 \\ \end{bmatrix}\]
Solving the equations by any method of your choice, we get
\[\begin{matrix} \Delta x = 0.5000 \\ \Delta y = - 3.500 \\ \end{matrix}\]
Since
\[\begin{matrix} \Delta x = x_{2} - x_{1} = 0.5000 \\ \Delta y = y_{2} - y_{1} = - 3.500 \\ \end{matrix}\]
we get
\[\begin{split} x_{2}&= x_{1} + 0.5000 \\ &= 2 + 0.5000 \\ &= 2.5000 \end{split}\]
\[\begin{split} y_{2}&= y_{1} + ( - 3.500) \\ &= - 4 + ( - 3.500) \\ &= - 7.500 \end{split}\]
The absolute relative approximate errors at the end of the first iteration are
\[\begin{split} \left| \varepsilon_{a} \right|_{x}&= \left| \frac{x_{2} - x_{1}}{x_{2}} \right| \times 100 \\ &= \left| \frac{2.500 - 2.000}{2.500} \right| \times 100 \\ &= 20.00\% \end{split}\]
\[\begin{split} \left| \varepsilon_{a} \right|_{y} &= \left| \frac{y_{2} - y_{1}}{y_{2}} \right| \times 100\\ &= \left| \frac{- 7.500 - ( - 4.000)}{- 7.500} \right| \times 100 \end{split}\]
Iteration 2
The estimate of the root at the end of iteration#1 is
\[(x_{2},y_{2}) = (2.500 - 7.500)\]
Hence
\[\begin{bmatrix} 2(2.500) & 2( - 7.500) \\ 1 & - 1 \\ \end{bmatrix}\begin{bmatrix} \Delta x \\ \Delta y \\ \end{bmatrix} = \begin{bmatrix} - (2.500)^{2} - ( - 7.500)^{2} + 50 \\ - (2.500) + ( - 7.500) + 10 \\ \end{bmatrix}\]
\[\begin{bmatrix} 5 & - 15 \\ 1 & - 1 \\ \end{bmatrix}\begin{bmatrix} \Delta x \\ \Delta y \\ \end{bmatrix} = \begin{bmatrix} - 12.50 \\ 0 \\ \end{bmatrix}\]
Solving the above equations by any method of your choice gives
\[\Delta x = 1.250\]
\[\Delta y = 1.250\]
Since
\[\Delta x = x_{3} - x_{2} = 1.250\]
\[\Delta y = y_3 - y_2 = 1.250\]
giving
\[\begin{split} x_3 &= x_2 +1.250\\ &=2.500 + 1.250\\ &=3.750 \end{split}\]
\[\begin{split} y_{3} &= y_{2} + 1.250\\ &=-7.500 + 1.250\\ &=-6.250 \end{split}\]
The absolute relative approximate error at the end of the second iteration is
\[\begin{split} \left| \epsilon_{a} \right|_{x} &= \left| \frac{x_{3} - x_{2}}{x_{3}} \right| \times 100\\ &= \left| \frac{3.750 - 2.5}{3.750} \right| \times 100\\ &= 33.33\% \end{split}\]
\[\begin{split} \left| \epsilon_{a} \right|_{y} &= \left| \frac{y_{3} - y_{2}}{y_{3}} \right| \times 100\\ &= \left| \frac{-6.250 - (-7.500)}{-6.250}\right| \times 100\\ &= 20.00\% \end{split}\]
Although not asked in the example problem statement, the estimated values of the root and the absolute relative approximate errors are given below in Table 1.
Table 1: Estimate of the root and absolute relative approximate error.
| Iteration number, \(i\) | \(x_{i}\) | \(y_{i}\) | \(\left| \epsilon_{a} \right|_{x}\%\) | \(\left| \epsilon_{a} \right|_{y}\%\) |
|---|---|---|---|---|
| \(1\) | \(2.500\) | \(-7.500\) | \(20.00\) | \(46.67\) |
| \(2\) | \(3.750\) | \(-6.250\) | \(33.33\) | \(20.00\) |
| \(3\) | \(4.375\) | \(-5.625\) | \(14.29\) | \(11.11\) |
| \(4\) | \(4.688\) | \(-5.312\) | \(6.667\) | \(5.882\) |
| \(5\) | \(4.844\) | \(-5.156\) | \(3.226\) | \(3.030\) |
| \(6\) | \(4.922\) | \(-5.078\) | \(1.587\) | \(1.538\) |
The exact solution to which the above scheme is converging to is \((x,y) = (5, - 5)\)
Example 2
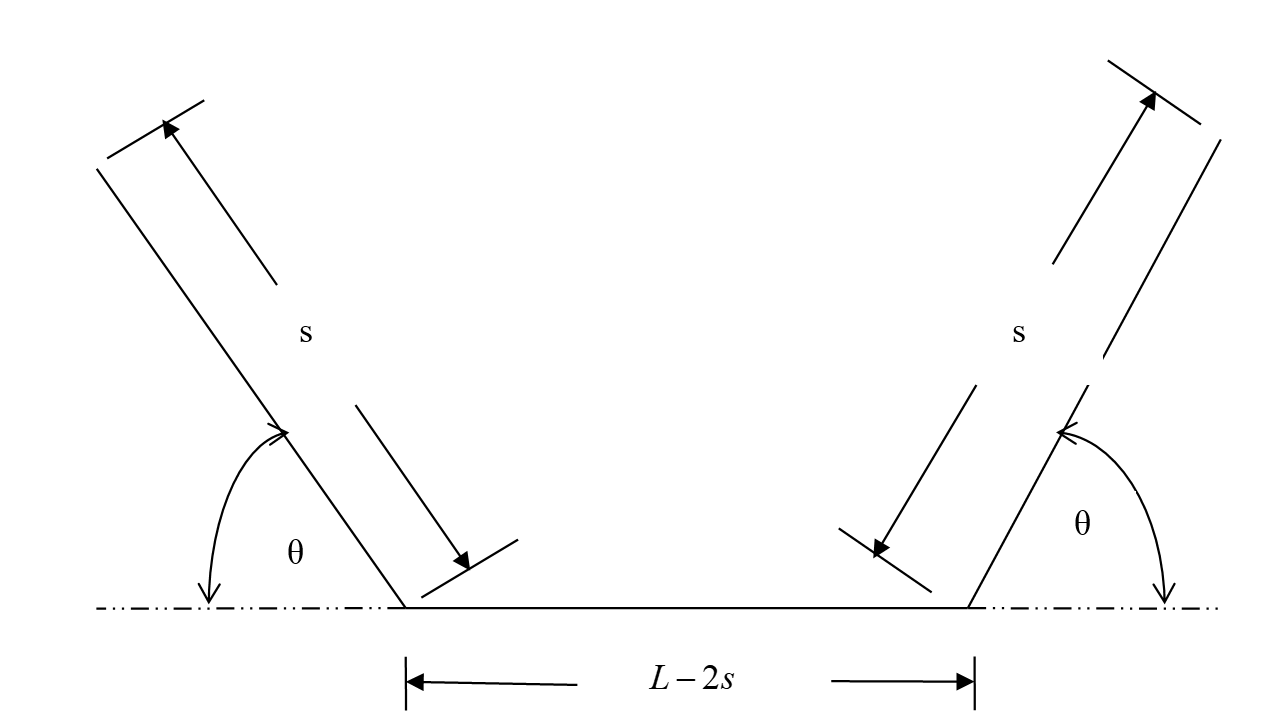
A \(5 \text{ m}\) long gutter is made from a flat sheet of aluminum which is \(5\ \text{m} \times 0.21\ \text{m}\). The shape of the gutter cross-section is shown in Figure 1 and is made by bending the sheet at two locations at an angle \(\theta\) (Figure 2). What are the values of \(s\) and \(\theta\), that will maximize the volume capacity of the gutter so that it drains water quickly during a heavy rainfall?
Figure 1 Sheet metal bent to form a gutter
Figure 2: Labeling the parameters and points of the gutter
Solution
One needs to maximize the cross-sectional area of the gutter. The cross-sectional area \(G\) of the gutter is given by
\[\begin{split} G &= \text{Area of trapezoid}\ \text{ABCD}\\ &= \frac{1}{2}(\text{AB} + \text{CD})(\text{FC})\;\;\;\;\;\;\; (E2.1)\end{split}\]
where
\[\text{AB}\ = \ L - 2\ s\;\;\;\;\;\;\; (E2.2)\]
\[\begin{split} CD &= AB + EA + BF\\ &= (L - 2s) + s\cos(\theta) + s\cos(\theta)\\ &= (L - 2s)\ + \ 2s\cos(\theta)\;\;\;\;\;\;\; (E2.3) \end{split}\]
\[\begin{split} FC &= BC \sin(\theta)\\ &= s\sin(\theta)\;\;\;\;\;\;\; (E2.4) \end{split}\]
hence
\[G = \frac{1}{2}(AB\ + CD) (DE)\]
\[\begin{split} G(s,\theta) &= \frac{1}{2}\left\lbrack (L - 2s) + (L - 2s) + 2s\cos(\theta) \right\rbrack s \sin(\theta)\\ &= \left\lbrack L - 2s + s\cos(\theta) \right\rbrack\ s\sin(\theta)\;\;\;\;\;\;\; (E2.5) \end{split}\]
For example, for \(\theta = 0{^\circ}\), the cross-sectional area of the gutter becomes
\[G = 0\]
as it represents a flat sheet, for \(\theta = 180{^\circ}\), the cross-sectional area of the gutter becomes
\[G = 0\]
as it represents an overlapped sheet, and for \(\theta = 90{^\circ}\), it represents a rectangular cross-sectional area with
\[G = (L - 2s) s\]
For the given \(L = 0.21\ \text{m,}\)
\[G(s,\theta) = (0.21 - 2s + s\cos\theta)s\sin\theta\]
Then
\[\frac{\partial G}{\partial s} = - s^{2}\sin^{2}\theta + (0.21 - 2s + s\cos\theta)s\cos\theta\]
\[\frac{\partial G}{\partial\theta} = ( - 2 + \cos\theta)s\sin\theta + (0.21 + 2s + s\cos\theta)\sin\theta\]
By solving the equations
\[f_{1}(s,\theta) = - s\sin^{2}\theta + (0.21 - 2s + s\cos\theta)s\cos\theta = 0\]
\[f_{2}(s,\theta) = ( - 2 + \cos\theta)s\sin\theta + (0.21 - 2s + s\cos\theta)\sin\theta = 0\]
we can find the local minimas and maximas of \(G(s,\theta)\). One of the local maximas may also be the absolute maximum. The values of \(s\) and \(\theta\) that correspond to the maximum of \(G(s,\theta)\) are what we are looking for. Can you solve the equations to find the corresponding values of \(s\) and \(\theta\) for maximum value of \(G\)? Intuitively, what do you think would be these values of \(s\) and \(\theta\)?
Appendix A: General matrix form of solving simultaneous nonlinear equations.
The general system of equations is given by
\[\begin{split} &f_{1}(x_{1},x_{2},...,x_{n}) = 0\\ &f_{2}(x_{1},x_{2},...,x_{n}) = 0\\ &\text{...}\\ &\text{...}\\ &\text{...}\\ &f_n(x_1,x_2,...,x_n) = 0\;\;\;\;\;\;\; (A.1)\end{split}\]
We can rewrite in a form as
\[F(\overset{\land}{x}) = \widehat{0}\;\;\;\;\;\;\; (A.2)\]
where
\[F(\overset{\land}{x}) = \begin{bmatrix} f_{1}(\overset{\land}{x}) \\ f_{2}(\overset{\land}{x}) \\ . \\ . \\ f_{n}(\overset{\land}{x}) \\ \end{bmatrix}\;\;\;\;\;\;\;(A.3)\]
\[\overset{\land}{0} = \begin{bmatrix} 0 \\ 0 \\ . \\ . \\ 0 \\ \end{bmatrix}\;\;\;\;\;\;\; (A.4)\]
\[\overset{\land}{x} = \begin{bmatrix} x_{1} \\ x_{2} \\ . \\ . \\ x_{n} \\ \end{bmatrix}^{T}\;\;\;\;\;\;\; (A.5)\]
The Jacobian of the system of equations by using Newton-Raphson method then is
\[J(x_{1},x_{2},...,x_{n}) = \begin{bmatrix} &\displaystyle\frac{\partial f_{1}}{\partial x_{1}}\ldots\frac{\partial f_{1}}{\partial x_{n}} \\ &.\ldots. \\ &.\ldots. \\ &.\ldots. \\ &\displaystyle\frac{\partial f_{n}}{\partial x_{1}}\ldots\frac{\partial f_{n}}{\partial x_{n}} \\ \end{bmatrix}\;\;\;\;\;\;\; (A.6)\]
Using the Jacobian for the Newton-Raphson method guess
\[\lbrack J\rbrack\Delta\overset{\land}{x} = - F(\overset{\land}{x})\;\;\;\;\;\;\; (A.7)\]
where
\[\Delta\overset{\land}{x} = {\overset{\land}{x}}_{\text{new}} - {\overset{\land}{x}}_{\text{old}}\;\;\;\;\;\;\; (A.8)\]
Hence
\[\Delta\overset{\land}{x} = - \lbrack J\rbrack^{- 1}F(\overset{\land}{x})\]
\[{\overset{\land}{x}}_{\text{new}} - {\overset{\land}{x}}_{\text{old}} = - \lbrack J\rbrack^{- 1}F(\overset{\land}{x})\]
\[{\overset{\land}{x}}_{\text{new}} = {\overset{\land}{x}}_{\text{old}} - \lbrack J\rbrack^{- 1}F(\overset{\land}{x})\;\;\;\;\;\;\; (A.10)\]
Evaluating the inverse of \(\lbrack J\rbrack\) in Equation (A.10) is computationally more intensive than solving Equation (A.7) for \(\Delta\overset{\land}{x}\)and calculating \({\overset{\land}{x}}_{\text{new}}\) as
\[{\overset{\land}{x}}_{\text{new}} = {\overset{\land}{x}}_{\text{old}} + \Delta\overset{\land}{x}\;\;\;\;\;\;\; (A.11)\]
Problem Set
(1). Solve the following set of nonlinear equations using Newton-Raphson method.
\[{xy = 2}\]
\[{x^{2} + y = 5}\] Start with an initial guess of \((3,4)\).
(2). Write the drawbacks of Newton-Raphson method and how you would address them.
(3). The following simultaneous nonlinear equations are found while modeling two continuous non-alcoholic stirred tank reactions
\[{f_{1} = (1 - R)\left\lbrack \frac{D}{10(1 + \beta_{1})} - \varphi_{1} \right\rbrack\exp\left( \frac{10\varphi_{1}}{1 + 10\varphi_{1}/\gamma} \right) - \varphi_{1}}\] \[{f_{2} = \varphi_{1} - (1 + \beta_{2})\varphi_{2} + (1 - R) \times \left\lbrack \frac{D}{10} - \beta_{1}\varphi_{1} - (1 + \beta_{2})\varphi_{2} \right\rbrack\exp\left( \frac{10\varphi_{2}}{1 + 10\varphi_{2}/\gamma} \right)}\]
Given \(\gamma = 1000,\ D = 22,\ \beta_{1} = 2,\ \beta_{2} = 2,\ R = 0.935\), find a suitable solution for \((\varphi_{1},\varphi_{2})\), given that \(\varphi_{i} \in \left\lbrack 0,1 \right\rbrack,i = 1,2\)
Source: Michael J. Hirsch, Panos M. Pardalos, Mauricio G.C Resende, Solving systems of nonlinear equations with continuous GRASP, Nonlinear Analysis: Real World Applications, Volume 10, Issue 4, August 2009, Pages 2000-2006, ISSN 1468-1218, http://dx.doi.org/10.1016/j.nonrwa.2008.03.006
(4). The Lorenz equations are given by
\[\frac{dx}{dt} = \sigma(y - x)\]
\[\frac{{dy}}{{dt}} = x(p - z) - y\]
\[\frac{dz}{dt} = xy - \beta{z}\]
Assuming \(\sigma = 3,\ p = 26,\ \beta = 1\), the steady state equations are written as
\[{0 = 3(y - x)}\] \[{0 = x(26 - z) - y}\] \[{0 = xy - z}\]
Write the Jacobian for the above system of equations.
(5). Use MATLAB or equivalent program to find the solution to the problem stated in Example 2.