Chapter 03.05: Secant Method of Solving Nonlinear Equations
Learning Objectives
After successful completion of this lesson, you should be able to:
1) derive the secant method to solve for the roots of a nonlinear equation,
2) use the secant method to numerically solve a nonlinear equation.
What is the secant method and why would I want to use it instead of the Newton-Raphson method?
The Newton-Raphson method of solving a nonlinear equation \(f(x) = 0\) is given by the iterative formula
\[x_{i + 1}\ = \ x_{i} - \frac{f(x_{i})}{f^{\prime}(x_{i})}\ \ \ (1)\]
One of the drawbacks of the Newton-Raphson method is that you have to evaluate the derivative of the function. With availability of symbolic manipulators such as Maple, MathCAD, MATHEMATICA and MATLAB, this process has become more convenient. However, it still can be a laborious process, and even intractable if the function is derived as part of a numerical scheme. To overcome these drawbacks, the derivative of the function, \(f(x)\) is approximated as
\[f^{\prime}(x_{i}) = \frac{f(x_{i}) - f(x_{i - 1})}{x_{i} - x_{i - 1}}\ \ \ (2)\]
Substituting Equation (2) in Equation (1) gives
\[x_{i + 1} = x_{i} - \frac{f(x_{i})(x_{i} - x_{i - 1})}{f(x_{i}) - f(x_{i - 1})}\ \ \ (3)\]
The above equation is called the secant method. This method now requires two initial guesses, but unlike the bisection method, the two initial guesses do not need to bracket the root of the equation. The secant method is an open method and may or may not converge. However, when secant method converges, it will typically converge faster than the bisection method. However, since the derivative is approximated as given by Equation (2), it typically converges slower than the Newton-Raphson method.
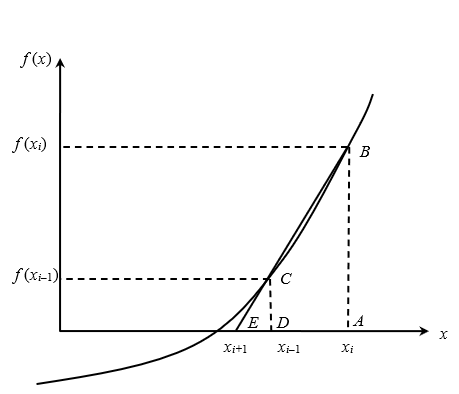
The secant method can also be derived from geometry, as shown in Figure 1. Taking two initial guesses, \(x_{i - 1}\) and \(x_{i}\), one draws a straight line between \(f(x_{i})\) and \(f(x_{i - 1})\) passing through the \(x\) -axis at \(x_{i + 1}\). ABE and DCE are similar triangles.
Hence
\[\frac{{AB}}{{AE}} = \frac{{DC}}{{DE}}\]
\[\frac{f(x_{i})}{x_{i} - x_{i + 1}} = \frac{f(x_{i - 1})}{x_{i - 1} - x_{i + 1}}\]
On rearranging, the secant method is given as
\[x_{i + 1} = x_{i} - \frac{f(x_{i})(x_{i} - x_{i - 1})}{f(x_{i}) - f(x_{i - 1})}\]
Figure 1 Geometrical representation of the secant method.
Application of Secant Method
Let’s take an example to show the application of the secant method to solve a nonlinear equation.
Example 1
You are working for ‘DOWN THE TOILET COMPANY’ that makes floats (Figure 2) for ABC commodes. The floating ball has a specific gravity of \(0.6\) and a radius of \(5.5\) cm. You are asked to find the depth to which the ball is submerged when floating in water.
The equation that gives the depth \(x\) to which the ball is submerged under water is given by
\[x^{3} - 0.165x^{2} + 3.993 \times 10^{- 4} = 0\]
Use the secant method of finding roots of equations to find the depth \(x\) to which the ball is submerged under water. Conduct three iterations to estimate the root of the above equation. Find the absolute relative approximate error and the number of significant digits at least correct at the end of each iteration.
Solution
\(f\left( x \right) = x^{3} - 0.165x^{2} + 3.993 \times 10^{- 4}\)
Let us assume the initial guesses of the root of \(f\left( x \right) = 0\) as \(x_{- 1} = 0.02\) and \(x_{0} = 0.05\).
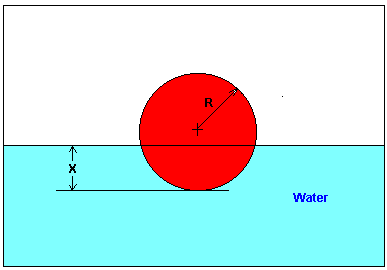
Figure 2 Floating ball problem.
Iteration 1
The estimate of the root is
\[\begin{split} x_{1} &=x_{0} - \frac{f\left( x_{0} \right)\left( x_{0} - x_{- 1} \right)}{f\left( x_{0} \right) - f\left( x_{- 1} \right)}\\ &= x_{0} - \frac{\left( x_{0}^{3} - 0.165x_{0}^{2} + 3.993 \times 10^{- 4} \right) \times \left( x_{0} - x_{- 1} \right)}{\left( x_{0}^{3} - 0.165x_{0}^{2} + 3.993 \times 10^{- 4} \right)^{} - \left( x_{- 1}^{3} - 0.165x_{- 1}^{2} + 3.993 \times 10^{- 4} \right)}\\ &= 0.05 - \frac{\left\lbrack 0.05^{3} - 0.165\left( 0.05 \right)^{2} + 3.993 \times 10^{- 4} \right\rbrack \times \left\lbrack 0.05 - 0.02 \right\rbrack}{\left\lbrack 0.05^{3} - 0.165\left( 0.05 \right)^{2} + 3.993 \times 10^{- 4} \right\rbrack^{} - \left\lbrack 0.02^{3} - 0.165\left( 0.02 \right)^{2} + 3.993 \times 10^{- 4} \right\rbrack}\\ &= 0.06461 \end{split}\]
The absolute relative approximate error \(\left| \epsilon_{a} \right|\) at the end of Iteration 1 is
\[\begin{split} \left| \epsilon_{a} \right| &= \left| \frac{x_{1} - x_{0}}{x_{1}} \right| \times 100\\ &= \left| \frac{0.06461 - 0.05}{0.06461} \right| \times 100\\ &= 22.62\% \end{split}\]
The number of significant digits at least correct is \(0\), as you need an absolute relative approximate error of \(5\%\) or less for one significant digit to be correct in your result.
Iteration 2
\[\begin{split} x_{2} &= x_{1} - \frac{f\left( x_{1} \right)\left( x_{1} - x_{0} \right)}{f\left( x_{1} \right) - f\left( x_{0} \right)}\\ &= \ x_{1} - \frac{\left( x_{1}^{3} - 0.165x_{1}^{2} + 3.993 \times 10^{- 4} \right) \times \left( x_{1} - x_{0} \right)}{\left( x_{1}^{3} - 0.165x_{1}^{2} + 3.993 \times 10^{- 4} \right)^{} - \left( x_{0}^{3} - 0.165x_{0}^{2} + 3.993 \times 10^{- 4} \right)}\\ &= 0.06461 - \frac{\left\lbrack 0.06461^{3} - 0.165\left( 0.06461 \right)^{2} + 3.993 \times 10^{- 4} \right\rbrack \times \left( 0.06461 - 0.05 \right)}{\left\lbrack 0.06461^{3} - 0.165\left( 0.06461 \right)^{2} + 3.993 \times 10^{- 4} \right\rbrack^{} - \left\lbrack 0.05^{3} - 0.165\left( 0.05 \right)^{2} + 3.993 \times 10^{- 4} \right\rbrack}\\ &= 0.06241 \end{split}\]
The absolute relative approximate error \(\left| \epsilon_{a} \right|\) at the end of Iteration 2 is
\[\begin{split} \left| \epsilon_{a} \right| &= \left| \frac{x_{2} - x_{1}}{x_{2}} \right| \times 100\\ &= \left| \frac{0.06241 - 0.06461}{0.06241} \right| \times 100\\ &= 3.525\% \end{split}\]
The number of significant digits at least correct is \(1\), as you need an absolute relative approximate error of \(5\%\) or less.
Iteration 3
\[\begin{split} x_{3} &= x_{2} - \frac{f\left( x_{2} \right)\left( x_{2} - x_{1} \right)}{f\left( x_{2} \right) - f\left( x_{1} \right)}\\ &= x_{2} - \frac{\left( x_{2}^{3} - 0.165x_{2}^{2} + 3.993 \times 10^{- 4} \right) \times \left( x_{2} - x_{1} \right)}{\left( x_{2}^{3} - 0.165x_{2}^{2} + 3.993 \times 10^{- 4} \right) - \left( x_{1}^{3} - 0.165x_{1}^{2} + 3.993 \times 10^{- 4} \right)^{}}\\ &= 0.06241 - \frac{\left\lbrack 0.06241^{3} - 0.165\left( 0.06241 \right)^{2} + 3.993 \times 10^{- 4} \right\rbrack \times \left( 0.06241 - 0.06461 \right)}{\left\lbrack 0.06241^{3} - 0.165\left( 0.06241 \right)^{2} + 3.993 \times 10^{- 4} \right\rbrack^{} - \left\lbrack 0.06461^{3} - 0.165\left( 0.06461 \right)^{2} + 3.993 \times 10^{- 4} \right\rbrack}\\ &= 0.06238 \end{split}\]
The absolute relative approximate error \(\left| \epsilon_{a} \right|\) at the end of Iteration 3 is
\[\begin{split} \left| \epsilon_{a} \right| &= \left| \frac{x_{3} - x_{2}}{x_{3}} \right| \times 100\\ &= \left| \frac{0.06238 - 0.06241}{0.06238} \right| \times 100\\ &= 0.0595\% \end{split}\]
The number of significant digits at least correct is \(2\), as you need an absolute relative approximate error of \(0.5\%\) or less. Table 1 shows the secant method calculations for the results from the above problem.
Table 1 Secant method results as a function of iterations.
| Iteration Number,n | \(x_{i-1}\) | \(x_i\) | \(x_{i+1}\) | \(|\epsilon_a|\) | \(f(x_{i+1})\) |
|---|---|---|---|---|---|
| \(1\) | \(0.02\) | \(0.05\) | \(0.06461\) | \(22.62\) | \(-1.9812 \times 10^{-5}\) |
| \(2\) | \(0.05\) | \(0.06461\) | \(0.06241\) | \(3.525\) | \(-3.285 \times 10^{-7}\) |
| \(3\) | \(0.06461\) | \(0.06241\) | \(0.06238\) | \(0.0595\) | \(2.0252 \times 10^{-9}\) |
| \(4\) | \(0.06241\) | \(0.06238\) | \(0.06238\) | \(3.64 \times 10^{-4}\) | \(-1.8576 \times 10^{-13}\) |
Multiple Choice Test
(1). The secant method of finding roots of nonlinear equations falls under the category of _____________ methods.
(A) bracketing
(B) graphical
(C) open
(D) random
(2). The secant method formula for finding the square root of a real number \(R\) from the equation \(x^{2} - R = 0\)is
(A) \(\displaystyle \frac{x_{i}x_{i - 1} + R}{x_{i} + x_{i - 1}}\)
(B) \(\displaystyle \frac{x_{i}x_{i - 1}}{x_{i} + x_{i - 1}}\)
(C) \(\displaystyle \frac{1}{2}\left( x_{i} + \frac{R}{x_{i}} \right)\)
(D) \(\displaystyle \frac{2x_{i}^{2} + x_{i}x_{i - 1} - R}{x_{i} + x_{i - 1}}\)
(3). The next iterative value of the root of \(x^{2} - 4 = 0\) using secant method, if the initial guesses are \(3\) and \(4\), is
(A) \(2.2857\)
(B) \(2.5000\)
(C) \(5.5000\)
(D) \(5.7143\)
(4). The root of the equation \(f\left( x \right) = 0\) is found by using the secant method. Given one of the initial estimates is \(x_{0} = 3\), \(f\left( 3 \right) = 5\), and the angle the secant line makes with the x-axis is \(57{^\circ}\), the next estimate of the root, \(x_{1}\), is
(A) \(-3.2470\)
(B) \(-0.24704\)
(C) \(3.247\)
(D) \(6.2470\)
(5). For finding the root of \(\sin\ x = 0\) by the secant method, the following choice of initial guesses would not be appropriate.
(A) \(\displaystyle \frac{\pi}{4}\ \text{and}\ \frac{\pi}{2}\)
(B) \(\displaystyle \frac{\pi}{4}\ \text{and}\ \frac{3\pi}{4}\)
(C) \(\displaystyle - \frac{\pi}{2}\ \text{and}\ \frac{\pi}{2}\)
(D) \(\displaystyle \frac{\pi}{3}\ \text{and}\ \frac{\pi}{2}\)
(6). When drugs are given orally to a patient, the drug concentration c in the blood stream at time \(t\) is given by a formula
\[c = Kte^{-{at}}\]
where \(K\) is dependent on parameters such as the dose administered while \(a\) is dependent on the absorption and elimination rates of the drug. If \(K = 2\) and \(a = 0.25\), and \(t\) is in seconds and \(c\) is in mg/ml, the time at which the maximum concentration is reached is given by the solution of the equation,
(A) \(2te^{- 0.25t} = 0\)
(B) \(2e^{- 0.25t} - 2te^{- 0.25t} = 0\)
(C) \(2e^{- 0.25t} - 0.5te^{- 0.25t} = 0\)
(D) \(2te^{- 0.25t} = 2\)
For complete solution, go to
http://nm.mathforcollege.com/mcquizzes/03nle/quiz_03nle_secant_solution.pdf
Problem Set
(1). Find the estimate of the root of \(x^{2} - 4 = 0\) by using secant method, if initial guesses of the roots are \(3\) and \(5\). Conduct three iterations. Also, calculate the approximate error, true error, absolute relative approximate error, and absolute relative true error at the end of each iteration.
(2). The velocity of a body is given by \(v(t) = 5e^{- t} + 6\), where \(v\) is in m/s and \(t\) is in seconds.
a) Use secant method to find when the velocity will be \(7.0\) m/s. Use only two iterations and take \(t = 2\) and \(t = 3.5\) seconds as the initial guesses.
b) What is the relative true error at the end of the second iteration for part (a)?
(3). You are working for DOWN THE TOILET COMPANY that makes floats for ABC commodes. The ball has a specific gravity of \(0.6\) and has a radius of \(5.5\) cm. You are asked to find the depth to which the ball will get submerged when floating in water.
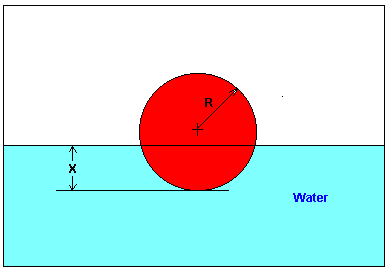
The equation that gives the depth \(x\) (unit of \(x\) is in m) to which the ball is submerged under water is given by
\[x^{3} - 0.165x^{2} + 3.993 \times 10^{- 4} = 0\]
Solving it exactly would require some effort. However using numerical techniques such as secant method, we can solve this equation and any other equation of the form \(f(x) = 0\). Solve the above equation by secant method and do the following.
a) Conduct three iterations. Use initial guesses of \(0.055\) and \(0.0825\).
b) Calculate the absolute relative approximate error at the end of each step.
c) Find the number of significant digits that are at least correct at the end of each iteration.
d) How could you have used the knowledge of the physics of the problem to develop initial guesses for the secant method?
(4). The root of the equation \(f(x) = 0\) is found by using secant method. The initial guesses for the root are assumed to be \(x_{0} = 3\) and \(x_{1} = 2\). Given \(f(3) = 28\) and \(f(2) = 4\), what is the
a) angle the secant makes with the \(x\) -axis,
b) next estimate of the root, \(x_{2}\).
(5). The root of the equation \(f(x) = 0\) is found by using secant method. If the initial estimates of the root are \(x_{0} = 5.0\) and \(x_{1} = 2.0\), and the angle the secant makes with the \(x\) -axis between \(x_{0} = 5.0\) and \(x_{1} = 2.0\) is \(88.75^{\circ}\). If the next estimate of the root is \(x_{2} = 1.9130\), what is the value of the function \(f(x)\) at \(x = 2\)?
(6). Find the secant method formula for finding the square root of a real number \(R\) from the equation \(x^{2} - R = 0\). Use the formula to find the square root of \(50.41\). Assume \(50.41\) and \(25.205\) as the initial guesses. How many iterations does it take to get at least \(3\) significant digits correct in your answer? Do not calculate the true value to answer the question.