2.2 Derivation

The Newton-Raphson method is based on the principle that if the initial guess of the root of \(f(x)=0\) is at \(x_i\), then if one draws the tangent to the curve at \(f(x_i)\), the point \(x_{i+1}\) where the tangent crosses the x-axis is an improved estimate of the root (Figure 1). One can then use \(x_{i+1}\) as the next point to draw the tangent line to the function \(f(x)\) and find out where that tangent line crosses the x-axis. Continuing this process brings us closer and closer to the root of the equation.

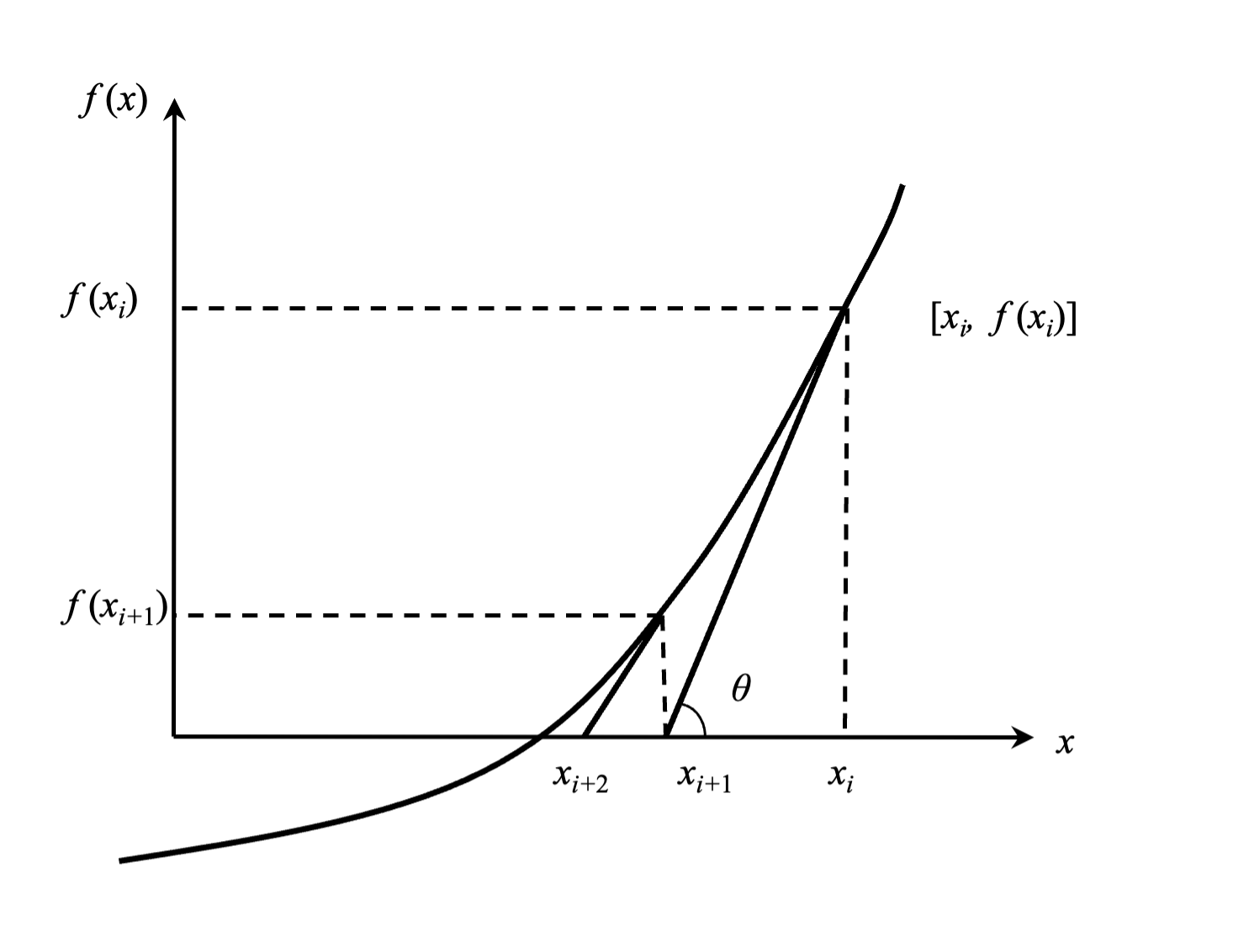
Figure 1 Geometrical illustration of the Newton-Raphson method

Using the definition of the slope of a function, at \(x=x_i\)

\(f'(x_i) = tanθ\)

     \(= \frac{f(x_i )-0}{x_i-x_{i+1}}\),

which gives \(x_{i+1} = x_i - \frac{f(x_i )}{f'(x_i)}\)       \((1)\)

Equation (1) is called the Newton-Raphson formula for solving nonlinear equations of the form \(f(x)=0\). So starting with an initial guess, \(x_i\), one can find the next guess, \(x_{i+1}\), by using Equation (1). One can repeat this process until one finds the root within a desirable tolerance.