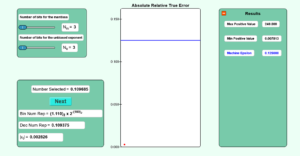
Description: This simulation shows you how a real number is represented in binary floating-point format and shows how the absolute relative true error in its representation is bound by the machine epsilon.
Keywords: binary, base-2, base-10, conversion between bases, floating-point, machine epsilon.
Learning Objectives: After successful completion of running the simulation with the student would be able to 1) find out the representation of a randomly chosen number based on the number of bits used for the mantissa and the exponent 2) show the absolute relative true error in the representation 3) verify that this error is bound by the machine epsilon.
Full Resources: The full resources for the topic of the floating-point binary representation are given here which include textbook content, a PowerPoint presentation, a multiple-choice test, audiovisual lectures, and application examples.
Software Requirements: Latest versions of Safari, Microsoft Edge, Firefox, Google Chrome.
Credits: Design Team: Autar Kaw. Software development: Mayank Pandey.
We acknowledge the immense help of the Phet Google group, third party libraries: almond-0.2.9.js, easing-equations-r12,FileSaver-b8054a2.js, fontawesome-webfont-3.0.2.svg, jama-1.0.2, jquery-2.1.0.js, lodash-2.4.1.js, pegjs-0.7.0.js, seedrandom-2.4.2.js, text-2.0.12.js, Tween-r12.js
Acknowledgments: This material is based upon work supported partially by the National Science Foundation under Grant Number 2013271. Any opinions, findings, and conclusions, or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation.
All Simulations: Here is the link for all the simulations developed.
