Chapter 05.02: Direct Method of Interpolation
Learning Objectives
After successful completion of this lesson, you should be able to:
1) find the interpolant through the direct method,
2) choose the correct data points for interpolation,
3) solve problems using the direct method of interpolation,
4) use the direct method interpolants to find derivatives of discrete functions,
5) use the direct method interpolants to find integrals of discrete functions.
Direct Method
The direct method (also called the Vandermonde polynomial method) of interpolation is based on the following premise. Given \(n + 1\) data points, fit a polynomial of order \(n\) as given below
\[y = a_{0} + a_{1}x + \ldots \ldots \ldots \ldots \ldots + a_{n}x^{n}\;\;\;\;\;\;\;\;\;\;\;\; (1)\]
through the data, where \(a_{0},a_{1},\ldots \ldots \ldots ,a_{n}\) are \(n + 1\) real constants. Since \(n + 1\) values of \(y\) are given at \(n + 1\) values of \(x\), one can write \(n + 1\) equations. Then the \(n + 1\) constants, \(a_{0},a_{1},\ldots \ldots \ldots ,a_{n}\) can be found by solving the \(n + 1\) simultaneous linear equations. To find the value of \(y\) at a given value of \(x\), simply substitute the value of \(x\) in Equation 1.
But, it is not necessary to use all the data points. How does one then choose the order of the polynomial and what data points to use? This concept of choosing points and the direct method of interpolation are best illustrated using examples.
Example 1
The upward velocity of a rocket is given as a function of time in Table 1.
Table 1. Velocity as a function of time.
| \(t\ (\text{s})\) | \(v(t)\ (\text{m/s})\) |
|---|---|
| \(0\) | \(0\) |
| \(10\) | \(227.04\) |
| \(15\) | \(362.78\) |
| \(20\) | \(517.35\) |
| \(22.5\) | \(602.97\) |
| \(30\) | \(901.67\) |
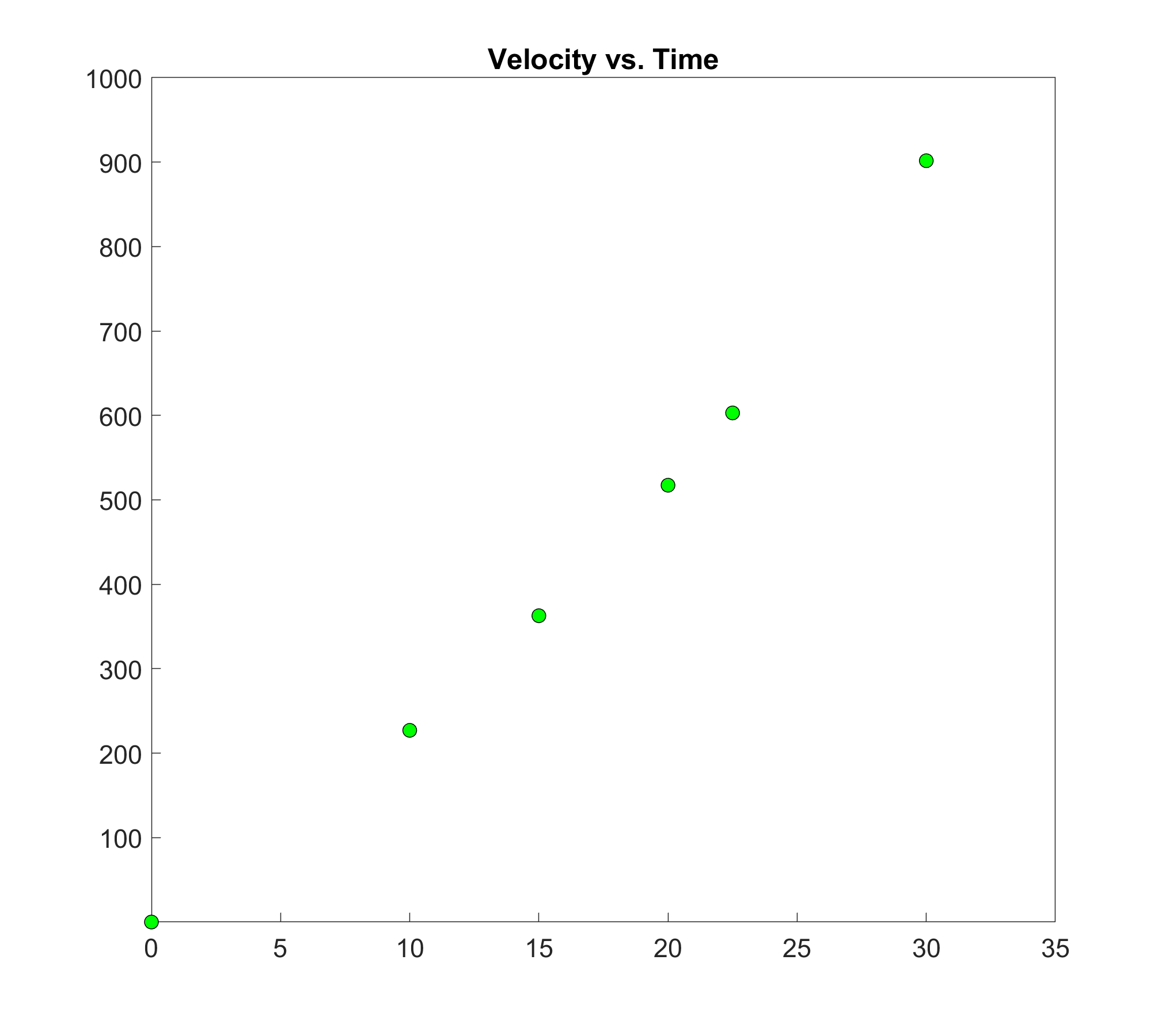
Figure 1. Graph of velocity vs. time data for the rocket example.
Estimate the velocity at \(t = 16\) seconds using the direct method of interpolation with a first-order polynomial.
Solution
For first-order polynomial interpolation (also called linear interpolation), the velocity given by
\[v\left( t \right) = a_{0} + a_{1}t\;\;\;\;\;\;\;\;\;\;\;\; (E1.1)\]
Figure 2. Linear interpolation.
Since we want to find the velocity at \(t = 16\), and we are using a first-order polynomial, we need to choose the two data points that are closest to \(t = 16\) that also bracket \(t = 16\) to evaluate it. The two points are \(t_{0} = 15\) and \(t_{1} = 20\).
Then
\[\begin{split} t_{0} &= 15,\ v\left( t_{0} \right) = 362.78\\ t_{1} &= 20,\ v\left( t_{1} \right) = 517.35 \end{split}\]
Equation (E1.1) gives
\[\begin{split} v\left( 15 \right) = a_{0} + a_{1}\left( 15 \right) &= 362.78\\ v\left( 20 \right) = a_{0} + a_{1}\left( 20 \right) &= 517.35 \end{split}\]
Writing the equations in matrix form, we have
\[\begin{bmatrix} 1 & 15 \\ 1 & 20 \\ \end{bmatrix}\begin{bmatrix} a_{0} \\ a_{1} \\ \end{bmatrix} = \begin{bmatrix} 362.78 \\ 517.35 \\ \end{bmatrix}\]
Solving the above two equations gives
\[\begin{split} a_{0} &= - 100.93\\ a_{1} &= 30.914\end{split}\]
Hence from Equation (E1.1)
\[\begin{split} v\left( t \right) &= a_{0} + a_{1}t\\ &= - 100.93 + 30.914t,\ 15 \leq t \leq 20 \end{split}\]
At \(t = 16\),
\[\begin{split} v\left( 16 \right) &= - 100.92 + 30.914 \times 16\\ &= 393.70\ \text{m/s} \end{split}\]
Example 2
The upward velocity of a rocket is given as a function of time in Table 2.
Table 2. Velocity as a function of time.
| \(t\ (\text{s})\) | \(v(t)\ (\text{m/s})\) |
|---|---|
| \(0\) | \(0\) |
| \(10\) | \(227.04\) |
| \(15\) | \(362.78\) |
| \(20\) | \(517.35\) |
| \(22.5\) | \(602.97\) |
| \(30\) | \(901.67\) |
a) Estimate the velocity at \(t = 16\) seconds using the direct method of interpolation with a second-order polynomial.
b) Find the absolute relative approximate error for the second-order polynomial approximation.
c) Using the second-order polynomial interpolant for velocity from part (a), find the distance covered by the rocket from \(t = 11\ s\) to \(t = 16\ s\).
d) Using the second-order polynomial interpolant for velocity from part (a), find the acceleration of the rocket at \(t = 16\ s\).
Solution
For second-order polynomial interpolation (also called quadratic interpolation), the velocity is given by
\[v\left( t \right) = a_{0} + a_{1}t + a_{2}t^{2}\;\;\;\;\;\;\;\;\;\;\;\; (E2.1)\]
Figure 3. Quadratic interpolation.
a) Since we want to find the velocity at \(t = 16\), and we are using a second-order polynomial, we need to choose the three data points that are closest to \(t = 16\) that also bracket \(t = 16\) to evaluate it. The three points are \(t_{0} = 10,\ \ t_{1} = 15,\ \text{and}\ t_{2} = 20\).
Then
\[\begin{split} t_{0} &= 10,\ v\left( t_{0} \right) = 227.04\\ t_{1} &= 15,\ v\left( t_{1} \right) = 362.78\\ t_{2} &= 20,\ v\left( t_{2} \right) = 517.35 \end{split}\]
Equation (E2.1) gives
\[\begin{split} v\left( 10 \right) &= a_{0} + a_{1}\left( 10 \right) + a_{2}\left( 10 \right)^{2} = 227.04\\ v\left( 15 \right) &= a_{0} + a_{1}\left( 15 \right) + a_{2}\left( 15 \right)^{2} = 362.78\\ v\left( 20 \right) &= a_{0} + a_{1}\left( 20 \right) + a_{2}\left( 20 \right)^{2} = 517.35 \end{split}\]
Writing the three equations in matrix form, we have
\[\begin{bmatrix} 1 & 10 & 100 \\ 1 & 15 & 225 \\ 1 & 20 & 400 \\ \end{bmatrix}\begin{bmatrix} a_{0} \\ a_{1} \\ a_{2} \\ \end{bmatrix} = \begin{bmatrix} 227.04 \\ 362.78 \\ 517.35 \\ \end{bmatrix}\]
Solving the above three equations gives
\[\begin{split} a_{0} &= 12.050\\ a_{1} &= 17.733\\ a_{2} &= 0.37660 \end{split}\]
Hence from Equation (E2.1)
\[v\left( t \right) = 12.050 + 17.733t + 0.37660t^{2},\ 10 \leq t \leq 20\;\;\;\;\;\;\;\;\;\;\;\; (E2.2)\]
At \(t = 16\),
\[\begin{split} v\left( 16 \right) &= 12.050 + 17.7333\left( 16 \right) + 0.37660\left( 16 \right)^{2}\\ &= 392.19\ \text{m/s} \end{split}\]
b) The absolute relative approximate error \(\left| \epsilon_{a} \right|\) obtained between the results from the first- and second- order polynomial is
\[\begin{split} \left| \epsilon_{a} \right| &= \left| \frac{392.19 - 393.70}{392.19} \right| \times 100\\ &= 0.38410\% \end{split}\]
c) The distance covered by the rocket between \(t = 11\ s\) and \(t = 16\ s\) can be calculated from the interpolating polynomial (Equation E2.2)
\[v\left( t \right) = 12.050 + 17.733t + 0.37660t^{2},\ 10 \leq t \leq 20\]
Note that the polynomial is valid between \(t = 10\ \text{s}\) and \(t = 22.5\ \text{s}\) and hence includes the limits of integration of \(t = 11\ \text{s}\) and \(t = 16\ \text{s}\) can
So
\[\begin{split} s\left( 16 \right) - s\left( 11 \right) &= \int_{11}^{16}{v\left( t \right){dt}}\\ &= \int_{11}^{16}{(12.050 + 17.733t + 0.3766{0t}^{2})\ }{dt}\\ &= \left\lbrack 12.050t + 17.733\frac{t^{2}}{2} + 0.37660\frac{t^{3}}{3} \right\rbrack_{11}^{16}\\ &= 1604.3\ \text{m} \end{split}\]
d) The acceleration at \(t = 16\ \text{s}\) is given by
\[a\left( 16 \right) = \left.\frac{d}{{dt}}v \left( t \right) \right|_{t = 16}\]
Given that from Equation (E2.2)
\[v\left( t \right) = 12.050 + 17.733t + 0.3766{0t}^{2},\ 10 \leq t \leq 20\]
we get
\[\begin{split} a\left( t \right) &= \frac{d}{\text{dt}}v\left( t \right)\\ &= \frac{d}{\text{dt}}\left( 12.050 + 17.733t + 0.37660t^{2} \right)\\ &= 17.733 + 0.75320t,\ 10 \leq t \leq 20 \end{split}\]
Hence
\[\begin{split} a\left( 16 \right) &= 17.733 + 0.75320(16)\\ &= 29.784\ \text{m/s}^{2} \end{split}\]
Example 3
The upward velocity of a rocket is given as a function of time in Table 3.
Table 3. Velocity as a function of time.
| \(t\ (\text{s})\) | \(v(t)\ (\text{m/s})\) |
|---|---|
| \(0\) | \(0\) |
| \(10\) | \(227.04\) |
| \(15\) | \(362.78\) |
| \(20\) | \(517.35\) |
| \(22.5\) | \(602.97\) |
| \(30\) | \(901.67\) |
a) Determine the value of the velocity at \(t = 16\) seconds using the direct method of interpolation with a third-order polynomial.
b) Find the absolute relative approximate error for the third-order polynomial approximation.
c) Using the third-order polynomial interpolant for velocity from part (a), find the distance covered by the rocket from \(t = 11\ s\) to \(t = 16\ s\).
d) Using the third-order polynomial interpolant for velocity from part (a), find the acceleration of the rocket at \(t = 16\ s\).
Solution
a) For third-order polynomial interpolation (also called cubic interpolation), we choose the velocity given by
\[v \left( t \right) = a_{0} + a_{1}t + a_{2}t^{2} + a_{3}t^{3}\;\;\;\;\;\;\;\;\;\;\;\; (E3.1)\]
Figure 4. Cubic interpolation.
Since we want to find the velocity at \(t = 16\), and we are using a third-order polynomial, we need to choose the four data points closest to \(t = 16\) that also brackets \(t = 16\) to evaluate it.
The four points are \(t_{0} = 10,t_{1} = 15,\ t_{2} = 20\) and \(t_{3} = 22.5\).
Then
\[\begin{split} t_{0} &= 10,\ v\left( t_{0} \right) = 227.04\\ t_{1} &= 15,\ v\left( t_{1} \right) = 362.78\\ t_{2} &= 20,\ v\left( t_{2} \right) = 517.35\\ t_{3} &= 22.5,\ v\left( t_{3} \right) = 602.97\end{split}\]
Equation (E3.1)
\[\begin{split} v\left( 10 \right) &= a_{0} + a_{1}\left( 10 \right) + a_{2}\left( 10 \right)^{2} + a_{3}\left( 10 \right)^{3} = 227.04\\ v\left( 15 \right) &= a_{0} + a_{1}\left( 15 \right) + a_{2}\left( 15 \right)^{2} + a_{3}\left( 15 \right)^{3} = 362.78 \\ v\left( 20 \right) &= a_{0} + a_{1}\left( 20 \right) + a_{2}\left( 20 \right)^{2} + a_{3}\left( 20 \right)^{3} = 517.35 \\ v\left( 22.5 \right) &= a_{0} + a_{1}\left( 22.5 \right) + a_{2}\left( 22.5 \right)^{2} + a_{3}\left( 22.5 \right)^{3}= 602.97 \end{split}\]
Writing the four equations in matrix form, we have
\[\begin{bmatrix} 1 & 10 & 100 & 1000 \\ 1 & 15 & 225 & 3375 \\ 1 & 20 & 400 & 8000 \\ 1 & 22.5 & 506.25 & 11391 \\ \end{bmatrix}\begin{bmatrix} a_{0} \\ a_{1} \\ a_{2} \\ a_{3} \\ \end{bmatrix} = \begin{bmatrix} 227.04 \\ 362.78 \\ 517.35 \\ 602.97 \\ \end{bmatrix}\]
Solving the above four equations gives
\[\begin{split} a_{0} &= - 4.2540\\ a_{1} &= 21.266\\ a_{2} &= 0.13204\\ a_{3} &= 0.0054347\end{split}\]
Hence
\[\begin{split} v\left( t \right) &= a_{0} + a_{1}t + a_{2}t^{2} + a_{3}t^{3}\\ &= - 4.2540 + 21.266t + 0.13204t^{2} + 0.0054347t^{3},\ 10 \leq t \leq 22.5 \end{split}\;\;\;\;\;\;\;\;\;\;\;\; (E3.2)\]
From Equation (E3.2)
\[\begin{split} v\left( 16 \right) &= - 4.2540 + 21.266\left( 16 \right) + 0.13204\left( 16 \right)^{2} + 0.0054347\left( 16 \right)^{3}\\ &= 392.06\ \text{m/s} \end{split}\]
b) The absolute percentage relative approximate error \(\left| \epsilon_{a} \right|\) for the value obtained for \(v(16)\) between second and third-order polynomial is
\[\begin{split} \left| \epsilon_{a} \right| &= \left| \frac{392.06 - 392.19}{392.06} \right| \times 100\\ &= 0.033269\% \end{split}\]
c) The distance covered by the rocket between \(t = 11\ s\) and \(t = 16\ s\) can be calculated from the interpolating polynomial (Equation E3.2)
\[v\left( t \right) = - 4.2540 + 21.266t + 0.13204t^{2} + 0.0054347t^{3},\ 10 \leq t \leq 22.5\]
Note that the polynomial is valid between \(t = 10\ \text{s}\) and \(t = 22.5\ \text{s}\) and hence includes the limits of integration of \(t = 11\ \text{s}\) and \(t = 16\ \text{s}\).
So
\[\begin{split} s\left( 16 \right) - s\left( 11 \right) &= \int_{11}^{16}{v\left( t \right)\{dt}\\ &= \int_{11}^{16}{( - 4.2540 + 21.266t + 0.13204t^{2} + 0.0054347t^{3})\ }{dt}\\ &= \left\lbrack - 4.2540t + 21.266\frac{t^{2}}{2} + 0.13204\frac{t^{3}}{3} + 0.0054347\frac{t^{4}}{4} \right\rbrack_{11}^{16}\\ &= 1605.0\ \text{m} \end{split}\]
- The acceleration at \(t = 16\ \text{s}\) is given by
\[a\left( 16 \right) = \left.\frac{d}{{dt}}v \left( t \right) \right|_{t = 16}\]
Given that from Equation (E3.2)
\[v\left( t \right) = - 4.2540 + 21.266t + 0.13204t^{2} + 0.0054347t^{3},\ 10 \leq t \leq 22.5\]
we get
\[\begin{split} a\left( t \right) &= \frac{d}{{dt}}v\left( t \right)\\ &= \frac{d}{{dt}}\left( - 4.2540 + 21.266t + 0.13204t^{2} + 0.0054347t^{3} \right)\\ &= 21.266 + 0.26408t + 0.016304t^{2},\ 10 \leq t \leq 22.5 \end{split}\]
Hence
\[\begin{split} a\left( 16 \right) &= 21.266 + 0.26408\left( 16 \right) + 0.016304\left( 16 \right)^{2}\\ &= 29.665\ \text{m/s}^{2} \end{split}\]
Multiple Choice Test
(1). Given \(n + 1\) data pairs, a unique polynomial of degree ________________ passes through \(n + 1\) data points.
(A) \(n + 1\)
(B) \(n + 1\) or less
(C) \(n\)
(D) \(n\) or less
(2). The data of the velocity of a body as a function of time is given as follows.
| Time \((s)\) | \(0\) | \(15\) | \(18\) | \(22\) | \(24\) |
| Velocity \((m/s)\) | \(22\) | \(24\) | \(37\) | \(25\) | \(123\) |
The velocity in m/s at \(16{s}\) using linear polynomial interpolation is most nearly
(A) \(27.867\)
(B) \(28.333\)
(C) \(30.429\)
(D) \(43.000\)
(3). The following data of the velocity of a body as a function of time is given as follows.
| Time \((s)\) | \(0\) | \(15\) | \(18\) | \(22\) | \(24\) |
| Velocity \((m/s)\) | \(22\) | \(24\) | \(37\) | \(25\) | \(123\) |
The velocity in m/s at \(16{ s}\) using quadratic polynomial interpolation is most nearly
(A) \(27.867\)
(B) \(28.333\)
(C) \(30.429\)
(D) \(43.000\)
(4). The following data of the velocity of a body is given as a function of time
| Time, \(t\) \((s)\) | \(0\) | \(15\) | 18 | \(22\) | \(24\) |
| Velocity, \(v\) \((m/s)\) | \(22\) | 24 | \(37\) | \(25\) | \(123\) |
Using quadratic interpolation, the interpolant
\(v\left( t \right) = 8.667t^{2} - 349.67t + 3523,\ 18 \leq t \leq 24\)
approximates the velocity of the body. From this information, one of the times in seconds at which the velocity of the body is 35 m/s during the above time interval of \(t = 18{s}\) to \(t = 24{s}\) is
(A) \(18.667\)
(B) \(20.850\)
(C) \(22.200\)
(D) \(22.294\)
(5). The following data of the velocity of a body is given as a function of time
| Time, \(t\) \((s)\) | \(0\) | \(15\) | \(18\) | \(22\) | \(24\) |
| Velocity, \(v\) \((m/s)\) | \(22\) | \(24\) | \(37\) | \(25\) | \(123\) |
One of the interpolant approximations for the velocity from the above data is given as
\[v(t) = 8.6667t^{2} - 349.67t + 3523,\ 18 \leq t \leq 24\]
Using the above interpolant, the distance in meters covered by the body between \(t = 19s\) and \(t = 22s\) is most nearly
(A) \(10.337\)
(B) \(88.500\)
(C) \(93.000\)
(D) \(168.00\)
(6). The following data of the velocity of a body is given as a function of time.
| Time \((s)\) | \(0\) | \(15\) | \(18\) | \(22\) | \(24\) |
| Velocity \((m/s)\) | \(22\) | \(24\) | \(37\) | \(25\) | \(123\) |
If you were going to use quadratic interpolation to find the value of the velocity at \(t = 14.9s\) , what three data points of time would you choose for interpolation?
(A) \(0, 15, 18\)
(B) \(15, 18, 22\)
(C) \(0, 15, 22\)
(D) \(0, 18, 24\)
For complete solution, go to
http://nm.mathforcollege.com/mcquizzes/05inp/quiz_05inp_direct_solution.pdf
Problem Set
(1). The following data of the velocity of a body as a function of time is given
| \(\text{Time}\ (s)\) | \(0\) | \(15\) | \(18\) | \(22\) | \(24\) |
|---|---|---|---|---|---|
| \(\text{Velocity}\ (m/s)\) | \(22\) | \(24\) | \(37\) | \(25\) | \(123\) |
What is the velocity at \(t = 14\) seconds using linear polynomial interpolation?
Answer: \(23.86\ m/s\)
(2). The following data of the velocity of a body as a function of time is given
| \(\text{Time}\ (s)\) | \(0\) | \(15\) | \(18\) | \(22\) | \(24\) |
|---|---|---|---|---|---|
| \(\text{Velocity}\ (m/s)\) | \(22\) | \(24\) | \(37\) | \(25\) | \(123\) |
What is the velocity at \(t = 14\) seconds using quadratic polynomial interpolation?
Answer: \(20.60\ m/s\)
(3). The following data of the velocity of a body as a function of time is given
| \(\text{Time}\ (s)\) | \(0\) | \(15\) | \(18\) | \(22\) | \(24\) |
|---|---|---|---|---|---|
| \(\text{Velocity}\ (m/s)\) | \(22\) | \(24\) | \(37\) | \(25\) | \(123\) |
What is the velocity at \(t = 14\) seconds using cubic polynomial interpolation?
Answer: \(17.30\ m/s\)
(4). The following data of the velocity of a body as a function of time is given as follows.
| \(\text{Time}\ (s)\) | \(0\) | \(15\) | \(18\) | \(22\) | \(24\) |
|---|---|---|---|---|---|
| \(\text{Velocity}\ (m/s)\) | \(22\) | \(24\) | \(37\) | \(25\) | \(123\) |
Using quadratic interpolation, the interpolant
\[v(t) = 9.500t^{2} - 383.0t + 3853\]
approximates the velocity of the body between 18 and 24 seconds. From this information, can you find out when the velocity of the body is 26 m/s during the above time interval?
Answer: \(18.287\ s \ \text{or}\ 22.028\ s\)
(5). The following data of the velocity of a body as a function of time is given as follows.
| \(\text{Time}\ (s)\) | \(0\) | \(15\) | \(18\) | \(22\) | \(24\) |
|---|---|---|---|---|---|
| \(\text{Velocity}\ (m/s)\) | \(22\) | \(24\) | \(37\) | \(25\) | \(123\) |
Find the value of velocity at \(t = 16\) seconds using the following interpolation function for the velocity of the body
\[v(t) = a_{0} + a_{1}\sin(t) + a_{2}\sin(2t)\]
where \(a_{0},\ a_{1},\) and \(a_{2}\) are the unknown constants.
Answer: \(24.875\ m/s\) (Intermediate answers \(a_0=25.008\), \(a_1=-9.2636\); \(a_2=-5.0770\) (arguments of sin are radians )
(6). You are given data for the upward velocity of a rocket as a function of time in the table below.
| \(t\ (s)\) | \(0\) | \(10\) | \(15\) | \(20\) | \(22.5\) | \(30\) |
|---|---|---|---|---|---|---|
| \(v(t)\ (m/s)\) | \(0\) | \(227.04\) | \(362.78\) | \(517.35\) | \(602.97\) | \(901.67\) |
a) Determine the value of the velocity at \(t = 16\) seconds using first order polynomial direct method.
b) Determine the value of the velocity at \(t = 16\) seconds using second order polynomial direct method. Find the absolute relative approximate error for approximation from the second order polynomial. How many significant digits would you at least trust in the solution?
c) Determine the value of the velocity at \(t = 16\) seconds using third order polynomial direct method. Find the absolute relative approximate error for approximation from the third order polynomial. How many significant digits would you at least trust in the solution?
d) What is the true error for part (a), (b) and (c), if I told you that the data given in the table above was derived from the formula
\[v(t) = 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100t} \right\rbrack - 9.8t,\quad 0 \leq t \leq 30\]
Answer: \(a)\ 393.69\ m/s\)
\(b)\ 392.19\ m/s,\ 0.38247\%,\ 2 \text{sig digits}\)
\(c)\ 392.05\ m/s,\ 0.035561\%,\ 3\ \text{sig digits}\)
\(d)\ \text{Exact}\ 392.08\ m/s\)
| Interpolant | True Error (\(E_t\)) |
|---|---|
| 1st order | \(-1.61\) |
| 2nd order | \(-0.11\) |
| 3rd order | \(0.03\) |
(7). You are given data for the upward velocity of a rocket as a function of time in the table below.
| \(t\ (s)\) | \(0\) | \(10\) | \(15\) | \(20\) | \(22.5\) | \(30\) |
|---|---|---|---|---|---|---|
| \(v(t)\ (m/s)\) | \(0\) | \(227.04\) | \(362.78\) | \(517.35\) | \(602.97\) | \(901.67\) |
a) Use linear interpolant approximation of velocity to find the acceleration at t = 16s.
b) Use quadratic interpolant approximation of velocity to find the acceleration at t = 16s.
c) Find the distance covered by the rocket from t =5s to 16s? Use any method.
Answer: \(a)\ 30.914\ m/s^2\)
\(b)\ 29.784\ m/s^2\)
\(c)\) Method 1: \(2672.3\ m\) by integrating 3rd order polynomial interpolant
Method 2: \(2704.2\ m\) by Trapezoidal rule with unequal segments
Other methods are possible too – average method is unacceptable.