Chapter 05.00: Physical Problem for Interpolation
Summary
The upward velocity of a rocket is given as a function of time at discrete data points. To find the velocity at a particular time requires interpolation.
Problem Statement
To find the altitude, velocity, and acceleration profile of a rocket, a velocity probe in the rocket (Figure 1) measures its velocity. Table 1 shows some typical values of the rocket velocity profile as a function of time.

Figure 1 A rocket launched into space: Source: NASA Langley Research Center, Office of Education, edu.larc.nasa.gov/pstp/
To determine the velocity at a particular time, one needs to interpolate the velocity vs. time data. Although you may be familiar with linear interpolation, where you draw a straight line between two data points, you also want to know how accurate your estimate is. This forces you to use other interpolation functions such as quadratic and cubic polynomials.
Table 1. Velocity as a function of time
| \(t\ (\text{s})\) | \(v(t)\ (\text{m/s})\) |
|---|---|
| \(0\) | \(0\) |
| \(10\) | \(227.04\) |
| \(15\) | \(362.78\) |
| \(20\) | \(517.35\) |
| \(22.5\) | \(602.97\) |
| \(30\) | \(901.67\) |
Can you also find the distance covered by the rocket from one point of time to another? Can you find the acceleration of the rocket at a particular time?
Summary
Find the coefficient of linear thermal expansion of steel at a specific temperature to estimate whether a steel shaft will cool down enough to shrink fit into a hollow hub. The coefficient of linear thermal expansion is to be found by using interpolation from a given table of coefficient of linear thermal expansion of steel as a function of temperature.
Problem Statement
To make the fulcrum (Figure 1) of a bascule bridge, a long hollow steel shaft called the trunnion is shrink fit into a steel hub.


Figure 1 Trunnion-Hub-Girder (THG) assembly.
This is done by first immersing the trunnion in a cold medium such as a dry-ice/alcohol mixture. After the trunnion reaches a steady-state temperature, that is, the temperature of the cold medium, the trunnion outer diameter contracts, is taken out and slid through the hole of the hub (Figure 2).


Figure 2 Trunnion slid through the hub after contracting
When the trunnion heats up, it expands and creates an interference fit with the hub. In 1995, on one of the bridges in Florida, this assembly procedure did not work as designed. Before the trunnion could be inserted fully into the hub, the trunnion got stuck. So a new trunnion and hub had to be ordered worth $50,000. Coupled with construction delays, the total loss ran into more than a hundred thousand dollars.
Why did the trunnion get stuck? This was because the trunnion had not contracted enough to slide through the hole.
Now the same designer is working on making the fulcrum for another bascule bridge. Can you help him so that he does not make the same mistake?
For this new bridge, he needs to fit a hollow trunnion of an outside diameter \(12.363^{\prime\prime}\) in a hub of an inner diameter \(12.358^{\prime\prime}\). His plan is to put the trunnion in dry-ice/alcohol mixture (the temperature of dry ice/alcohol mixture is \(- 108{^\circ}\text{F}\)) to contract the trunnion so that it can be slid through the hole of the hub. To slide the trunnion without sticking, he has also specified a diametral clearance of at least \(0.01^{\prime\prime}\). Assume the room temperature is \(80{^\circ}\text{F}\), is immersing it in a dry-ice/alcohol mixture a correct decision?
Solution
Looking at the records of the designer for the previous bridge where the trunnion got stuck in the hub, it was found that he used the coefficient of linear thermal expansion at room temperature to calculate the contraction in the trunnion diameter. In that case, the reduction, \(\Delta D\) in the outer diameter of the trunnion is
\[\Delta D = D\alpha\Delta T\;\;\;\;\;\;\;\;\;\;\;\; (1)\]
where
\[D = \text{outer diameter of the trunnion,}\]
\[\alpha = \text{coefficient of linear thermal expansion at room temperature,}\]
\[\Delta T =\text{change in temperature.}\]
Given
\[D = 12.363^{\prime\prime}\]
\[\alpha = 6.817 \times 10^{- 6}\ \text{in/in/}{^\circ}\text{F}\ \text{at}\ 80{^\circ}\text{F}\]
\[\begin{split} \Delta T &= T_{\text{fluid}} - T_{\text{room}}\\ &= - 108 - 80\\ &= - 188{^\circ}\text{F} \end{split}\]
where
\[T_{{fluid}}= \text{temperature of dry-ice/alcohol mixture}\]
\[T_{{room}}= \text{room temperature}\]
the reduction in the trunnion outer diameter is given by
\[\begin{split} \Delta D &= 12.363 \times \left( 6.47 \times 10^{- 6} \right)\left( - 188 \right)\\ &= - 0.01504^{\prime\prime} \end{split}\]
So the trunnion is predicted to reduce in diameter by \(0.01504^{\prime\prime}\). But is this enough reduction in diameter? As per the specifications, he needs the trunnion to contract by
\[\begin{split} &= \text{trunnion outside diameter} - \text{hub inner diameter} + \text{diametric clearance}\\ &=12.363^{\prime\prime} - 12.358^{\prime\prime} + 0.01^{\prime\prime}\\ &=0.015^{\prime\prime} \end{split}\]
So, according to his calculations, it is enough to put the steel trunnion in a dry-ice/alcohol mixture to get the desired contraction of \(0.015^{\prime\prime}\) as he is predicting a contraction of \(0.01504^{\prime\prime}\).
But as shown in the graph below, the coefficient of linear thermal expansion of steel decreases with temperature and is not constant over the range of temperature the trunnion goes through. Hence the above formula (Equation 1) would overestimate the thermal contraction. This assumption is the mistake he made in the calculations for the earlier bridge.
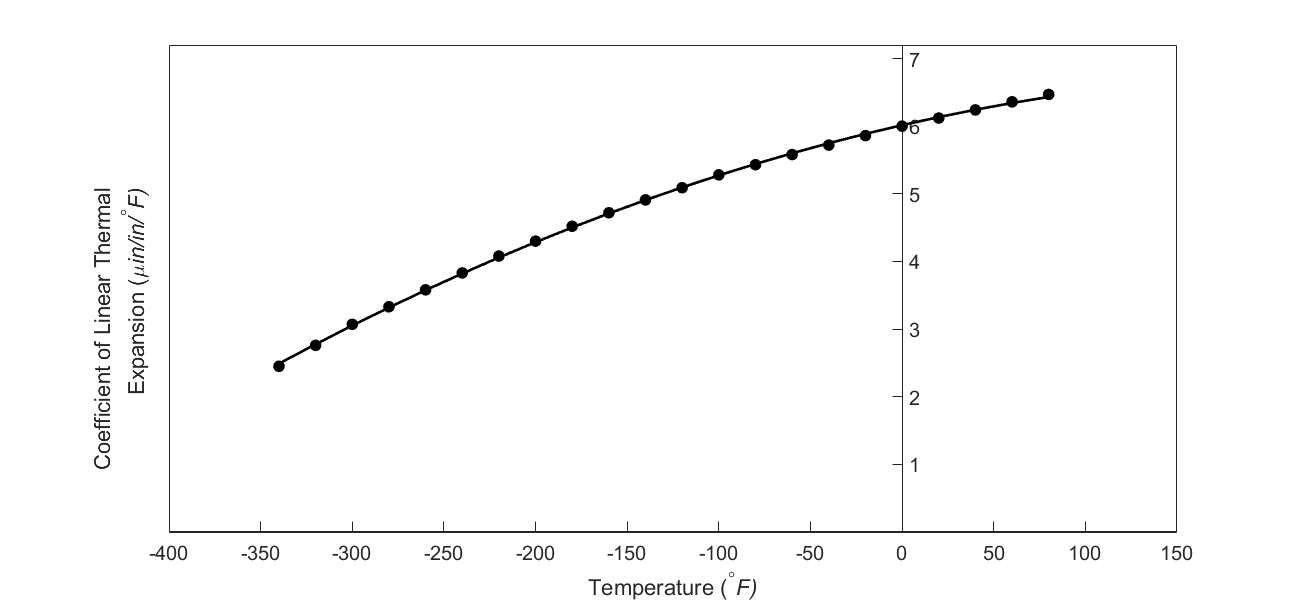
Figure 3 Varying coefficient of linear thermal expansion as a function of temperature for cast steel.
To get a better estimate of the contraction in the diameter, we can use the coefficient of linear thermal expansion value at the average temperature. The average temperature would be
\[\begin{split} T_{{avg}} &= \frac{- 108 + 80}{2}\\ &= -14^{\circ}\text{F} \end{split}\;\;\;\;\;\;\;\;\;\;\;\; (2)\]
Now given the table of coefficient of linear thermal expansion as a function of temperature as given below, we can use polynomial interpolation to find the coefficient of linear thermal expansion at the average temperature of \(- 14^{\circ}F\) and find the contraction using Equation (1).
Table 1 Coefficient of linear thermal expansion vs. temperature
| Temperature (\(^\circ \text{F}\)) | coefficient of linear thermal expansion (\({\mu}\text{in/in}{/}^{\circ}\text{F}\)) |
|---|---|
| \(80\) | \(6.47\) |
| \(60\) | \(6.36\) |
| \(40\) | \(6.24\) |
| \(20\) | \(6.12\) |
| \(0\) | \(6.00\) |
| \(-20\) | \(5.86\) |
| \(-40\) | \(5.72\) |
| \(-60\) | \(5.58\) |
| \(-80\) | \(5.43\) |
| \(-100\) | \(5.28\) |
| \(-120\) | \(5.09\) |
| \(-140\) | \(4.91\) |
| \(-160\) | \(4.72\) |
| \(-180\) | \(4.52\) |
| \(-200\) | \(4.30\) |
| \(-220\) | \(4.08\) |
| \(-240\) | \(3.83\) |
| \(-260\) | \(3.58\) |
| \(-280\) | \(3.33\) |
| \(-300\) | \(3.07\) |
| \(-320\) | \(2.76\) |
| \(-340\) | \(2.45\) |