|
Q1.
In
a general second order linear partial differential equation with two
independent variables,
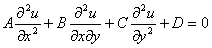
where A , B , C are
functions of x and
y,
and D
is a function of
x
, y ,
 , ,
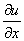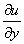then the PDE is elliptic if
B2-4AC<0
B2-4AC>0
B2-4AC=0
B2-4AC≠0
Q2.
The region in
which the following equation
acts as an
elliptic equation is
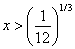
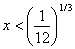
for all values of x
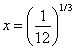
Q3. The
finite difference approximation of
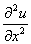 in
the elliptic equation
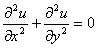
at
(x,y)
can be
approximated as
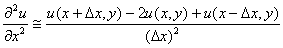
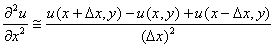
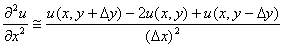
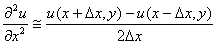
Q4.
Find the
temperature at the interior node given in the following figure using the
direct method
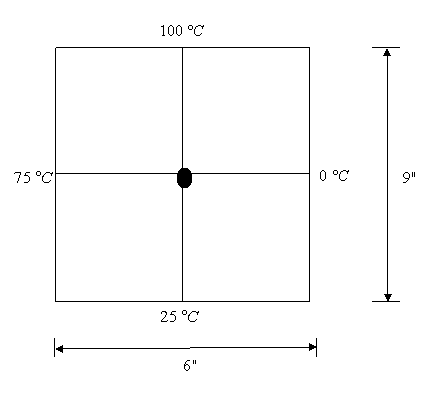
45.19
°C
48.64
°C
50.00
°C
56.79
°C
Q5. Find
the temperature at the interior node given in the following figure
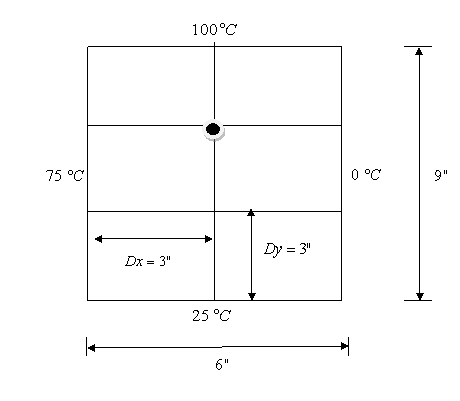
Using the
Lieberman method and relaxation factor of 1.2, the temperature at
x-=3, y=6
estimated after 2 iterations is (use the temperature of interior nodes
as 50°C
for the initial guess)
52.36
°C
53.57
°C
56.20
°C
58.64
°C
Q6.
Find the steady-state temperature at the interior node as given in the
following figure
53.57
°C
66.40
°C
68.20
°C
69.59
°C
Complete Solution
Multiple choice questions on other topics
|
