|
|
|
|
|
|
Pick the most
appropriate answer.
|
Q1.
When
using the transformed data model to find the constants of the regression
model 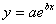 to
best fit to
best fit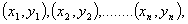 the
sum of the square of the residuals that is minimized is the
sum of the square of the residuals that is minimized is
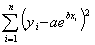
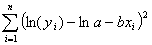
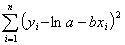
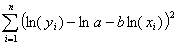
Q2.
It
is suspected from theoretical considerations that the rate of water flow from
a firehouse is proportional to some power of the nozzle pressure.
Assume pressure data is more accurate. You are transforming the data.
|
Flow rate, F
(gallons/min) |
96 |
129 |
135 |
145 |
168 |
235 |
|
Pressure, p (psi) |
11 |
17 |
20 |
25 |
40 |
55 |
The exponent of the power of the nozzle pressure in the regression
model F=apb
most nearly is
0.497
0.556
0.578
0.678
Q3. The transformed data model for the
stress-strain curve 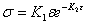 for
concrete in compression, where for
concrete in compression, where
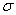 is
the stress and is
the stress and 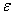 is
the strain is is
the strain is
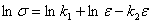
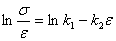
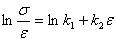
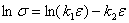
Q4.
In
nonlinear regression, finding the constants of the model requires
solving simultaneous nonlinear equations. However in the exponential
model 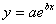 that
is best fit to that
is best fit to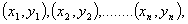 the
value of b can be found as a solution of a nonlinear equation.
That equation is given by the
value of b can be found as a solution of a nonlinear equation.
That equation is given by
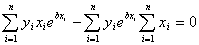
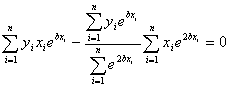
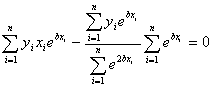
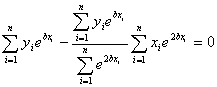
Q5. There
is a functional relationship between the mass density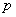 of
air and the altitude of
air and the altitude 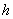 above
the sea level above
the sea level
|
Altitude above sea
level,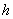 (km) (km) |
0.32 |
0.64 |
1.28 |
1.60 |
|
Mass Density,
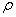 (kg/m3) (kg/m3) |
1.15 |
1.10 |
1.05 |
0.95 |
In the regression
model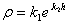 ,
the constant ,
the constant 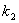 is
found as is
found as 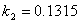 .
Assuming the mass density of air at the top of the atmosphere is .
Assuming the mass density of air at the top of the atmosphere is
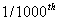 of
the mass density of air at sea level. The altitude in kilometers of the
top of the atmosphere most nearly is of
the mass density of air at sea level. The altitude in kilometers of the
top of the atmosphere most nearly is
46.2
46.6
49.7
52.5
Q6.
A steel
cylinder at 80oF of length 12" is placed in a
commercially available liquid nitrogen
bath -315oF
If the thermal expansion coefficient of steel behaves as a second order
polynomial of temperature and the polynomial is found by regressing the
data below,
|
Temperature
(oF) |
Thermal
expansion
coefficient
(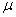 in/in/oF) in/in/oF) |
|
-320 |
2.76 |
|
-240 |
3.83 |
|
-160 |
4.72 |
|
-80 |
5.43 |
|
0 |
6.00 |
|
80 |
6.47 |
the
reduction in the length of the cylinder in inches most nearly is
0.0219
0.0231
0.0235
0.0307
Complete Solution
Multiple
choice questions on other topics
|
