Contents
COMPARING TWO SERIES FOR VALUE OF PI
Language : Matlab 2007a Authors : Autar Kaw Last Revised : October 30, 2008 Abstract: This program compares results for the value of pi using a) Gregory series and b) Ramanajun series
clc clear all clf format long disp('This program compares results for the value of') disp('pi using a) Gregory series and b) Ramanajun series') disp(' ') disp('Gregory series') disp('pi=sum over k from 0 to inf of (4*((-1)^k/(2*k+1))') disp(' ') disp('Ramanajun Series') disp('1/pi=sum over k from 0 to infinity of 2*sqrt(2)/9801*((4k)!*(1103+26390k)/(k!)^4*396^(4*k))')
This program compares results for the value of pi using a) Gregory series and b) Ramanajun series Gregory series pi=sum over k from 0 to inf of (4*((-1)^k/(2*k+1)) Ramanajun Series 1/pi=sum over k from 0 to infinity of 2*sqrt(2)/9801*((4k)!*(1103+26390k)/(k!)^4*396^(4*k))
INPUTS.
%If you want to experiment this the only parameter % you should and can change. % Maximum number of terms n=30;
PROGRAM
GREGORY SERIES
pi_gregory=0; for i=1:1:n pi_gregory=pi_gregory+(-1)^(i+1)*4*(1/(2*i-1)); pi_gregory_array(i)=pi_gregory; end
RAMANUJAN SERIES
pi_ram=0; for i=0:1:n-1 pi_ram=pi_ram+2*sqrt(2)/9801.0*(factorial(4*i))*(1103.0+26390.0*i)/((factorial(i)^4)*(396)^(4*i)); pi_ram_array(i+1)=1/pi_ram; end
THE OUTPUT
disp(' ') fprintf('\nNumber of Terms = %g',n) fprintf('\nGregory Series Value = %g',pi_gregory) fprintf('\nRamanujan Series Value = %g',1/pi_ram) disp( ' ')
Number of Terms = 30 Gregory Series Value = 3.10827 Ramanujan Series Value = 3.14159
PLOTTING THE TWO SERIES AS A FUNCTION OF TERMS
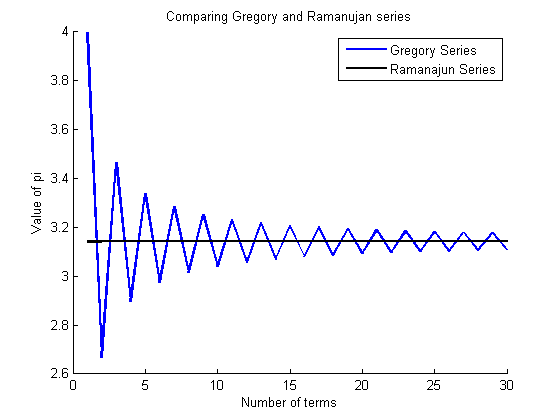
x=1:1:n; hold on xlabel('Number of terms') ylabel('Value of pi') title('Comparing Gregory and Ramanujan series') plot(x,pi_gregory_array,'color','blue','LineWidth',2) hold on plot(x,pi_ram_array,'color','black','LineWidth',2) legend('Gregory Series','Ramanajun Series',1)